Билинейные формы. Квадратичные формы.

Пусть V – линейное пространство над полем P. Функция, ставящая в соответствие паре векторов вещественное число, и обладающая свойствами линейности называется билинейной формой. Другими словами, функция называется билинейной, если

1. ,
2. ,

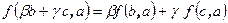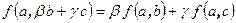где , .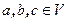

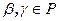Примером билинейной функции является скалярное произведение.

Теорема 4.1 Билинейная форма полностью определяется своими значениями на базисных векторах.

Доказательство. Пусть 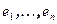- базис V. Разложим векторы b и c по базису 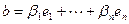, 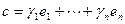. Тогда из линейности выводим . Теорема доказана.

Обозначим через 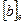столбец, составленный из координат вектора b, а через 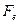– матрицу, на пересечении i-ой строки и j-го столбца которой расположено значение билинейной формы от базисных векторов 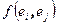. Легко убедиться в равенстве 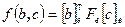. Матрица 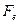называется матрицей билинейной формы f в базисе .

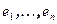Следствие 4.1 Билинейная форма полностью определяется своей матрицей.

Билинейная форма называется симметричной, если ее значение не меняется от перестановки аргументов, то есть .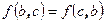

Следствие 4.2 Билинейная форма симметрична тогда и только тогда, когда найдется базис, в котором ее матрица симметрична.

Доказательство. Если билинейная форма симметричная, то в любом базисе ее матрица симметрична. Обратно, пусть в некотором базисе матрица билинейной формы симметричная. Тогда .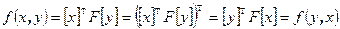

Квадратичной формой называется значение билинейной формы от одного аргумента, то есть f(x,x).

Одну и ту же квадратичную форму можно получить из разных билинейных форм. Например, квадратичную форму 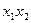можно получить из следующих билинейных форм , где .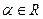

Между квадратичными формами и симметричными билинейными формами существует взаимно однозначное соответствие, определяемое формулой 0,25(f(x+y,x+y)-f(x-y,x-y)). Матрица симметричной билинейной формы, соответствующей квадратичной форме, называется матрицей квадратичной формы.