Нормальное псевдорешение.

Задача построения нормального псевдорешения сводится к решению системы 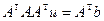и вычисления нормального псевдорешения по формуле .

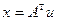Унитарное пространство.

Пусть V линейное пространство над полем комплексных чисел. Можно ли обобщить понятие скалярного произведения на такое пространство. Оказывается, да! Для этого достаточно незначительно изменить аксиомы скалярного произведения.

1. .

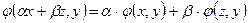2.

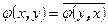
3. 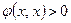при .

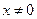Черта в свойстве 2 обозначает знак комплексного сопряжения. Пространство над полем комплексных чисел, в котором введено скалярное произведение называется унитарным.

Обозначим через G матрицу Грама базисных векторов, то есть матрицу на пересечении строки i столбца j стоит скалярное произведение i-го и j-го вектора 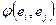. Используя матричные операции умножения, получаем 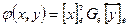. Матрицы Грама в разных базисах связаны формулой 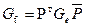, где P матрица перехода. Все остальные свойства скалярного произведения полностью сохраняются.

Билинейные функции, квадратичные формы.