Полуторалинейные формы. Эрмитовы формы.
Пусть V – линейное пространство над полем комплексных чисел C. Функция, ставящая в соответствие паре векторов комплексное число, и обладающая свойствами линейности по первому аргументами и «почти линейностью» по второму, называется полуторалинейной формой. Точнее, функция 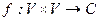 называется полуторалинейной, если
называется полуторалинейной, если
-
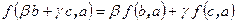 ,
, -
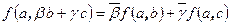 ,
,
где 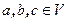 ,
, 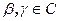 .
.
Примером полуторалинейной функции является скалярное произведение в унитарном пространстве.
Теорема 4.2. Полуторалинейная форма полностью определяется своими значениями на базисных векторах.
Доказательство. Пусть 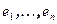 - базис V. Разложим векторы b и c по базису
- базис V. Разложим векторы b и c по базису 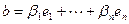 ,
, 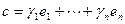 . Тогда
. Тогда 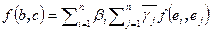 . Теорема доказана.
. Теорема доказана.
Обозначим через 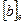 столбец, составленный из координат вектора b, а через
столбец, составленный из координат вектора b, а через 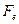 – матрицу, на пересечении i-ой строки и j-го столбца которой расположено значение полуторалинейной формы от базисных векторов
– матрицу, на пересечении i-ой строки и j-го столбца которой расположено значение полуторалинейной формы от базисных векторов 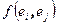 . Легко убедиться в равенстве
. Легко убедиться в равенстве 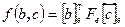 , где черта обозначает знак комплексного сопряжения. Матрица
, где черта обозначает знак комплексного сопряжения. Матрица 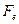 называется матрицей полуторалинейной формы f в базисе
называется матрицей полуторалинейной формы f в базисе 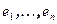 .
.
Следствие 4.3 Полуторалинейная форма полностью определяется своей матрицей.
Полуторалинейная форма называется эрмитовой, если ее значение меняется от перестановки аргументов на комплексно сопряженное, то есть 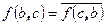 .
.
Следствие 4.4 Полуторалинейная форма является эрмитовой тогда и только тогда, когда найдется базис e, в котором ее матрица удовлетворяет равенству 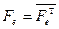 .
.
Для эрмитовых форм определен аналог квадратичной формы 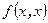 .
.
Значение квадратичной эрмитовой формы – всегда вещественное число, так как 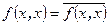 .
.
Дата добавления: 2016-05-25; просмотров: 792;
