Обоснование экспоненциальной устойчивости нелинейных систем с помощью функций Ляпунова, удовлетворяющих неравенствам – оценкам, характерным для квадратичных форм

В двух последних теоремах (и следствии из первой из них)доказано, что существование двух квадратичных форм

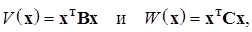(2.3.20)

связанных условиями (2.3.9)÷(2.3.11), являются условиями экспоненциальной устойчивости тривиального решения, необходимыми и достаточными для линейных однородных стационарных систем (ЛОСС) вида (2.3.1) и только достаточными и возможно, весьма далекими от необходимых («черезчур» (избыточно) достаточными [2,3]), для нелинейных нестационарных приведенных систем общего вида (2.1.1)÷(2.1.3), т.е. в такой системе тривиальное решение может быть экспоненциально устойчиво, а квадратичные формы, удовлетворяющие теореме о достаточных условиях экспоненциальной устойчивости, не могут быть найдены (не существуют).

Следовательно, класс функций Ляпунова, обеспечивающий необходимые и достаточные условия экспоненциальной устойчивости тривиального решения системы общего вида (2.1.1)÷(2.1.3), если он существует, должен быть шире класса квадратичных форм с постоянными параметрами.

Соответствующие теоретические результаты исследования экспоненциальной устойчивости нелинейных нестационарных систем были получены Н.Н. Красовским [2]. Рассмотрим их.

Определение. Функции Ляпунова 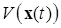, в общем случае, зависящие от времени, удовлетворяющие неравенствам – оценкам вида

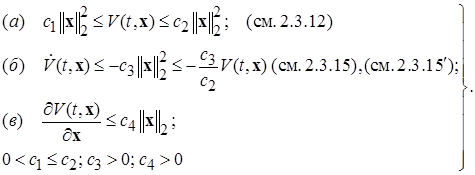(2.3.21)

называются функциями Ляпунова, удовлетворяющими неравенствам – оценкам, характерным для квадратичных форм, а сами соотношения (2.3.21) - неравенствам – оценкам, характерным для квадратичных форм, причем сами функции Ляпунова уже, в общем случае, не являются квадратичными формами с постоянными матрицами и коэффициенты 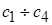в неравенствах (2.3.21) разумеется, не подчиняются, в общем случае, формулам (2.3.14), справедливым только для квадратичных форм. ■

Замечание. В неравенствах – оценках, характерных для квадратичных форм, два первых соотношения (а) и (б) упоминались ранее в (2.3.12) и (2.3.15) для случая квадратичных форм (2.3.10), (2.3.11), когда вычислялись по формулам (2.3.14), в то время, как неравенство –оценка (в) в (2.3.21) приводится впервые и является требованием, характерным для квадратичной формы. Покажем это. Пусть

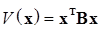
тогда

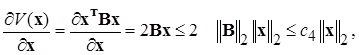
т.е. получим неравенство (2.3.21,в), где в частном случае квадратичной формы вычисляется по формуле (2.3.14).■

В данном определении установлен новый класс функций Ляпунова, удовлетворяющих неравенствам – оценкам, характерным для квадратичных форм, которые Н.Н. Красовский использовал при доказательстве следующей теоремы.

Теорема о необходимых и достаточных условиях экспоненциальной устойчивости тривиального решения нелинейных нестационарных приведенных систем общего вида (Н.Н. Красовский, 1959).

Пусть дана нелинейная нестационарная приведенная по Ляпунову система (2.1.1)÷(2.1.3) (см. п. 2.1). Повторим описание здесь:

Пусть дана приведенная по Ляпунову система

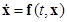(2.1.1)

с областью определения правых частей вида

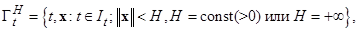(2.1.2)

причем функция удовлетворяет следующим свойствам в области (2.1.2):

а) f- непрерывна по t и x;

б) f- непрерывно дифференцируема по xи

(вследствие непрерывности по известной теореме

Вейерштрасса) все частные производные

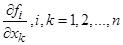, ограничены на любом компактном

подмножестве из области (2.1.2) (2.1.3)

в) 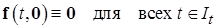, т.е. система

(2.1.1) допускает тривиальное решение .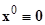

Тривиальное решение системы (2.1.1)÷(2.1.3) экспоненциально устойчиво при 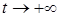равномерно на , т.е. по любому 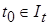все решения , удовлетворяющие неравенству

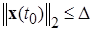(2.3.22)

с некоторой постоянной 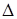, выбор которой не зависит от выбора 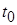, удовлетворяют и экспоненциальной оценке – неравенству вида

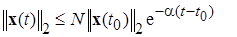(2.3.23)

тогда и только тогда, когда

в области

(2.3.24)

существует функция Ляпунова 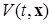, в общем случае зависящая от времени и удовлетворяющая неравенствам – оценкам, характерным для квадратичных форм, введенным в (2.3.21). При этом, введенные в (2.3.23) постоянные 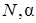- положительные числа, выбор которых не зависит от выбора решений 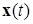, определяются соотношениями (2.3.18), а область экспоненциального притяжения (2.3.22) определяется оценкой (2.3.19). ■

Доказательство.

Достаточность теоремы доказана в теореме о достаточных условиях экспоненциальной устойчивости, рассмотренной в п. 2.3.1.

Доказательство необходимости подробно рассмотрено в книге [2, §11, 72-74], и здесь не приводится. □

Важное замечание. Поучительным будет привести примечание, которое автор этой теоремы Н.Н. Красовский помещает сразу после ее доказательства и которое здесь цитируется почти дословно по книге [2, с.74]. Экспоненциальная устойчивость, регламентирующая поведение траекторий системы экспоненциальной оценкой вида (2.3.23) является весьма естественной для линейных однородных стационарных систем вида (2.3.1), как было показано выше, однако в случае нелинейных нестационарных систем общего вида (2.1.1)÷(2.1.3) естественность этой оценки может вызвать сомнение. Следует, однако, иметь в виду, что единственным более или менее плодотворным путем исследования нелинейных систем является пока следующий путь – данную нелинейную систему сопоставляют с некоторыми похожими линейными системами, и таким путем выводятся критерии устойчивости для данной нелинейной системы. При таком подходе, естественно, и характер поведения траекторий устойчивой нелинейной системы оказывается подобным поведению траекторий вспомогательных линейных систем. Поэтому условие (2.3.23), а, следовательно, функция Ляпунова 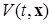с неравенствами – оценками вида (2.3.21), характерными для квадратичных форм, играют в теории устойчивости нелинейных систем значительно большую роль, чем это может показаться с первого взгляда (конец цитаты – курсив наш).

Надо ли говорить, что это глубокое замечание одного из ярких и плодотворных продолжателей методов исследования нелинейных систем, основанных на функциях Ляпунова, академика РАН Н.Н. Красовского (1924 – 2012 г.г) , высказанное им через 67 лет после опубликования в 1892 г. академиком А.М. Ляпуновым своего основного труда – докторской диссертации «Общая задача об устойчивости движения» [11], и сегодня, через 53 года после опубликования Н.Н. Красовским (в 1959 г.) своей известной книги «Некоторые задачи теории устойчивости движения» [2], остается актуальным.