Теорема о достаточных условиях экспоненциальной диссипативности нелинейной нестационарной системы с возмущением.

Пусть дана нелинейная нестационарная система «с возмущением» вида (2.4.1)÷(2.4.4). Для экспоненциальной диссипативности этой системы с областью диссипативности 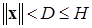и предельным множеством 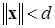достаточно существования функции Ляпунова 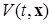, определенной и непрерывно дифференцируемой по 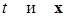всюду в области 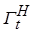вида (2.4.2) и такой, что:

1) для системы «без взвешивания» ( 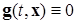) функция Ляпунова 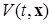удовлетворяет неравенствам-оценкам, характерным для квадратичных форм вида

(2.4.11)

2) для системы с «возмущением» полная производная функции Ляпунова 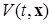, вычисленная в силу (2.4.1), подчинена неравенству вида

, (2.4.12)

где , g Î [0, 1).

Доказательство. Доказательство диссипативности рассмотрим для частного случая, когда в неравенстве (2.4.12) .

Пусть

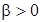, , , (2.4.13)

тогда после интегрирования (2.4.13) при 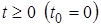будет

,

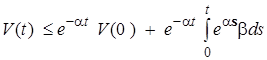и так как

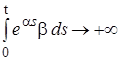при ,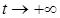

то получится предельное соотношение для верхнего предела вида

.

Таким образом, при 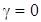из (2.4.12) следует неравенство для верхнего предела функции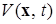

. (2.4.14)

Если

,

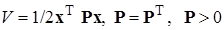т. е. V – положительно определенная квадратичная форма, то легко перейти к оценке предельного множества для траекторий x(t), а именно, как следует из (2.4.13):

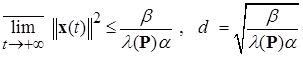, (2.4.15)

где 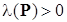– минимальное собственное значение матрицы .

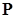В общем случае неравенства (2.4.12) при будет иметь место неравенство (без доказательства)

, (2.4.16)

и снова в случае квадратичной формы с постоянными коэффициентами для радиус предельного множества определится, как следует из соотношения (2.4.15), так:

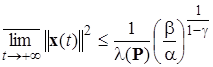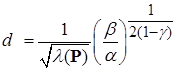; . (2.4.17)

Таким образом, из доказательства получили оценки (2.4.15), (2.4.17) предельных множеств диссипативности [10, с.140].□