Теорема о равномерной по (равномерной на устойчивости (К.П. Персидский, 1933).

Пусть дана приведенная система (2.1.1) ÷ (2.1.3). Если в некоторой области 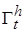существует функция Ляпунова 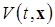, непрерывно дифференцируемая по t, x в этой области, и найдутся две независимых от времени положительно определенных функций Ляпунова вида 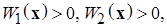таких что:

1) 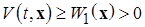(положительная определенность )

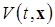2) 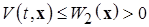(сильный БМВП при )

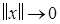3) 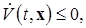(знакопостоянная отрицательная),

то тривиальное решение системы (2.1.1) устойчиво по Ляпунову при 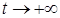равномерно по 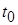(равномерно на )

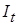(Без доказательства).

Замечание.Нетрудно видеть, что условия теоремы К.П. Персидского являются комбинацией требований к функции V и ее производной 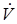, содержащихся в первой и второй теоремах Ляпунова, а именно, функция V здесь удовлетворяет второй теореме, а ее производная 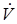- первой теореме.

В свете сказанного легко увидеть, что основные теоремы об устойчивости и асимптотической устойчивости содержат требования, удовлетворение которых придает поведению решений исследуемой системы свойства, не планируемые в определениях 1 и 2 (п. 1.2). В этом сказывается провиденческая сила второго метода.

Определение (равномерной асимптотической устойчивости). Тривиальное решение системы (2.1.1.)÷(2.1.3) называется асимптотически устойчивым равномерно по времени 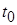и начальным возмущениям 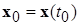, или просто равномерно асимптотически устойчивым, если оно асимптотически устойчиво при 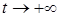с областью притяжения 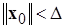(в смысле определения 2 (п. 1.2)) и, кроме того, для любого числа 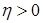можно указать положительное число 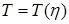(зависящее от выбора 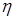), такое, что

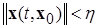, если ,

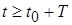каковы бы ни были начальный момент времени 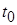и начальные возмущения 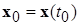из области притяжения .■

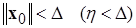Теорема о равномерной асимптотической устойчивости (Н.Н. Красовский, 1959)

Тривиальное решение системы (2.1.1.)÷(2.1.3) равномерно асимптотически устойчиво (в смысле данного определения), если выполняются все условия второй теоремы Ляпунова (асимптотической устойчивости). ■

Замечание. Таким образом, решения нелинейной системы, удовлетворяющей требования второй теоремы Ляпунова, облают свойствами, не запланированными в определении 2 (п. 2.1). Этот результат был замечен и доказан академиком Н.Н. Красовским (1959) [2]. Более того, можно указать оценку [3,4] времени Т

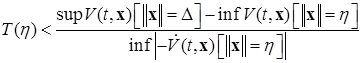(2.2.1)

приближения решения к тривиальному решению (говорят, к началу координат в 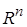, или просто к началу) при его переходе из 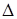-окрестности в 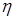-окрестность.■

Можно указать еще одно из направлений модификации теорем второго метода Ляпунова, связанного с важным свойством глобальной сходимости решений нелинейной системы, задаваемым определением 5 (п. 1.2).

Привлекая свойства ББНП при 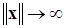(см. п. 1.4, определение 6), Е.А. Барбашин и Н.Н. Красовский доказали следующую теорему [2].

Теорема Барбашина – Красовского (о глобальной асимптотической устойчивости).

Пусть приведенная система (2.1.1) определена на полупространстве

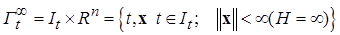(2.2.2)

или, как говорят, на всем 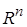, и пусть для нее в области определения (2.2.2) найдутся функция Ляпунова 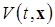и три не зависящие от времени функции Ляпунова.

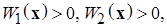и

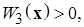
положительно определенные и такие, что:

1) 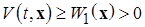(положительная определенность функции );

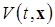2) 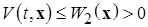(сильный БМВП при 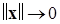функции );

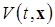3) 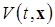допускает ББНП при 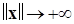(заметим, что условия (2) и (3) могут быть объединены в свойство существования бесконечного предела для ;

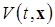4) 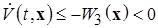(отрицательная определенность 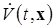, вычисленной в силу системы (2.1.1)).

Тогда тривиальное решение системы асимптотически устойчиво в целом, или глобально асимптотически устойчивости.■

Без доказательства (см. [2]).

Заканчивая этот краткий обзор, отметим, что математическая теория устойчивости систем, основанная на втором методе Ляпунова, особенно интенсивно начала развиваться в СССР, начиная с 1930-х годов, а за рубежом – начиная с 1950-х годов, когда прямой метод Ляпунова, сначала был, если можно так выразиться, «переоткрыт» советскими математиками и механиками (Н.Г. Четаев, И.Г. Малкин, А.И. Лурье, Г.Н. Дубошин, А.П. Тузов, Н.Н. Красовский, Е.А. Барбашин, В.И. Зубов, А.М. Летов, В.В. Румянцев, В.М. Матросов, В.А. Якубович и др.) а затем стал известен, благодаря их трудам, и за рубежом.

С тех пор в рамках развития второго метода Ляпунова было введено множество новых свойств и доказано множество новых результатов, связанных с уточнением и расширением понятия математической теории устойчивости, приложимых к различным областям знаний, обзору и и систематизации которых посвящена, например, монография [5], изложенная, вдобавок, на современном и лаконичном математическом языке.