Анализ устойчивости энергетической системы путём имитационного моделирования в среде matlab

Важной характеристикой систем электроснабжения является способность обеспечивать бесперебойное и качественное питание потребителей. Основным показателем качества является способность энергетической системы сохранять или восстанавливать свои свойства после различных нарушениях нормального режима работы, вызванного слабыми или сильными воздействиями на систему. Слабые воздействия на систему в основном обусловлены перегрузкой электроэнергетических систем. Токи элементов энергетических систем при таких воздействиях лишь в незначительной степени превышают номинальные значения. Устойчивость системы к слабым воздействиям оценивается коэффициентами статической устойчивости энергетической системы. Именно статическая устойчивость определяет возможность энергетической системы к сохранению работоспособности в условиях выхода из строя отдельных узлов электроэнергетической системы.

Нарушение нормального режима работы системы энергоснабжения может быть вызвано сильными воздействиями на систему. К сильным воздействиям на системы электроснабжения относят воздействия, связанные, как правило, с резким увеличением токов системы до значений, превышающих номинальные токи в десятки раз. Такие воздействия могут привести к нарушению динамической устойчивости, что сопровождается изменением частоты сети, резким колебаниям напряжения и переходу части генераторов системы в асинхронный режим работы.

При проектировании новых энергетических систем и при модернизации старых возникает острая необходимость в прогнозировании характеристик энергетических систем. Одним из путей определения устойчивости систем является теоретический анализ режимов работы при сильных и слабых воздействиях на систему. Учесть реальные параметры каждого элемента системы практически невозможно из-за их огромного количества и сложности взаимодействий этих параметров даже внутри каждого элемента. Необходимость решения проблемы приводит к значительной идеализации параметров элементов. Однако и идеализация параметров не всегда приводит к положительному результату из-за сложности самих систем электроснабжения.

Трудности, связанные с громоздкостью и сложностью теоретического анализа устойчивости электроэнергетических систем, вызывают желание разработчика переложить решение задач устойчивости на плечи компьютеров. В таком случае можно идти путём составления программ в одной из сред программирования или путём моделирования переходных процессов в одной из специально разработанных сред. Широкие возможности для моделирования энергосистем и процессов, происходящих в них, предоставляет пакет программ MatLab.

При анализе работы электрических систем необходимо учитывать не только электромагнитные параметры системы, но и связанные с ними механические параметры элементов системы, если эти параметры влияют на электромагнитные процессы в системе. Речь идёт прежде всего о первичных двигателях (турбинах), генераторах электрической энергии, автоматических регуляторах, двигателях нагрузки, где электрическая энергия, получаемая из распределительной сети системы, преобразуется в механическую. Следует отметить то, что под динамимической устойчивостью понимают способность системы восстанавливать после больших возмущений исходное состояние или практически близкое к исходному (допустимому по условиям эксплуатации системы). Под статической устойчивостью электрической системы понимается её способность восстанавливать исходный режим после кратковременного воздействия малого возмущения. В качестве параметров обычно принимают напряжение в узловых точках и токи в ветвях ЭС, а под возмущением понимают изменение механического момента на валу двигателя одного из генераторов или мощности нагрузки. Вследствие малости рассматриваемых возмущений, энергетическая система при анализе статической устойчивости может рассматриваться как линейная динамическая система. Нарушение статической устойчивости может происходить вследствие причин различной физической природы. Если мощность турбины, например, достигнет максимально возможного значения электромагнитной мощности генератора, происходит апериодическое нарушение устойчивости. При работе генератора в режиме холостого хода или при малой мощности, передаваемой через линию электропередач (ЛЭП), обладающую значительным активным сопротивлением, возможно самораскачивание турбогенератора. Аналогичное явление происходит в виде нарастающих колебаний угла при неправильной настройке автоматического регулятора возбуждения (АРВ). Это приводит к необходимости разработки эффективных методов и алгоритмов, обеспечивающих как высокое быстродействие, так и надежность получения результата. При оперативном управлении системой расчеты предельных режимов должны проводиться с учётом изменения схемно-режимной ситуации, а адекватная работа централизованных систем противоаварийной автоматики требует просмотра большого количества аварийных ситуаций за весьма короткое время, обусловленное значительной скоростью изменения параметров режима. Поэтому требуется разработка новых подходов, более полно учитывающих специфику задач оперативного управления.

Принципы анализа статической и динамической устойчивости продемонстрированы на примере электроэнергетической системы, состоящей из электростанции, представленной эквивалентным генератором G, повышающего трансформатора T1, двухцепной линии L1, L2, повышающего трансформатора T2 и сети бесконечной мощности NET. Такая схема подключения станции к энергетической системе является традиционной. Имитационная модель системы представлена на рисунке 1. По условным обозначениям, используемым в модели, не трудно определить местоположение перечисленных элементов системы. На модели представлены и контрольно-измерительные приборы, используемые для контроля электрических и механических параметров электроэнергетической системы. Для измерения электрических и механических величин генератора используется специальный измерительный блок, предназначенный для контроля параметров электрических машин MMD. На его вход подаётся информация с выхода m генератора. Между генератором и трансформатором T 1 включён комплект измерительных приборов, предназначенных для контроля режимов работы трёхфазных цепей KIP1. На выходе второго трансформатора включён аналогичный измерительный блок.

УСТОЙЧИВОСТЬ ЭЛЕКТРИЧЕСКИХ СИСТЕМ.

Деление режимов электрической цепи на установившиеся и переходные процессы условно. В установившемся режиме реальной системы её параметры постоянно меняются, что связано со следующими факторами [Л.5, с.169]:

· изменение нагрузки и реакцией на эти изменения регулирующих устройств;

· нормальными эксплуатационными изменениями схемы коммутации системы;

· включением и отключением отдельных генераторов или изменением их мощности.

Таким образом., в установившихся режимах в системе всегда возможны малые возмущения параметров её режима, при которых система должна оставаться устойчивой.

Статическая устойчивость – это способность системы восстанавливать исходный (или близкий к исходному) режим после малого его возмущения.

Динамическая устойчивость – это способность системы возвращаться в исходное (или близкое к нему) состояние после большого возмущения (аварийные режимы в электрической системе – КЗ, аварийные отключения или включения нагруженных агрегатов или линий, генераторов, транс-ров и т.п.), при этом возникают резкие изменения режима.

Исходя из определения статической устойчивости системы следует, что существует такой режим, при котором очень малое возмущение вызывает нарушение его устойчивости. Такой режим называется предельным, а нагрузки системы – максимальными или предельными нагрузками по условиям статической устойчивости.

Считается, что качество переходного процесса хорошее, если наблюдается быстрое его затухание и монотонность. Наибольшая величина отклонения параметра, при которой система ещё сохраняет устойчивость, определяет запас устойчивости, выражаемый коэффициентом запаса. Например, запас по напряжению и по мощности вычисляются по формулам:

, .

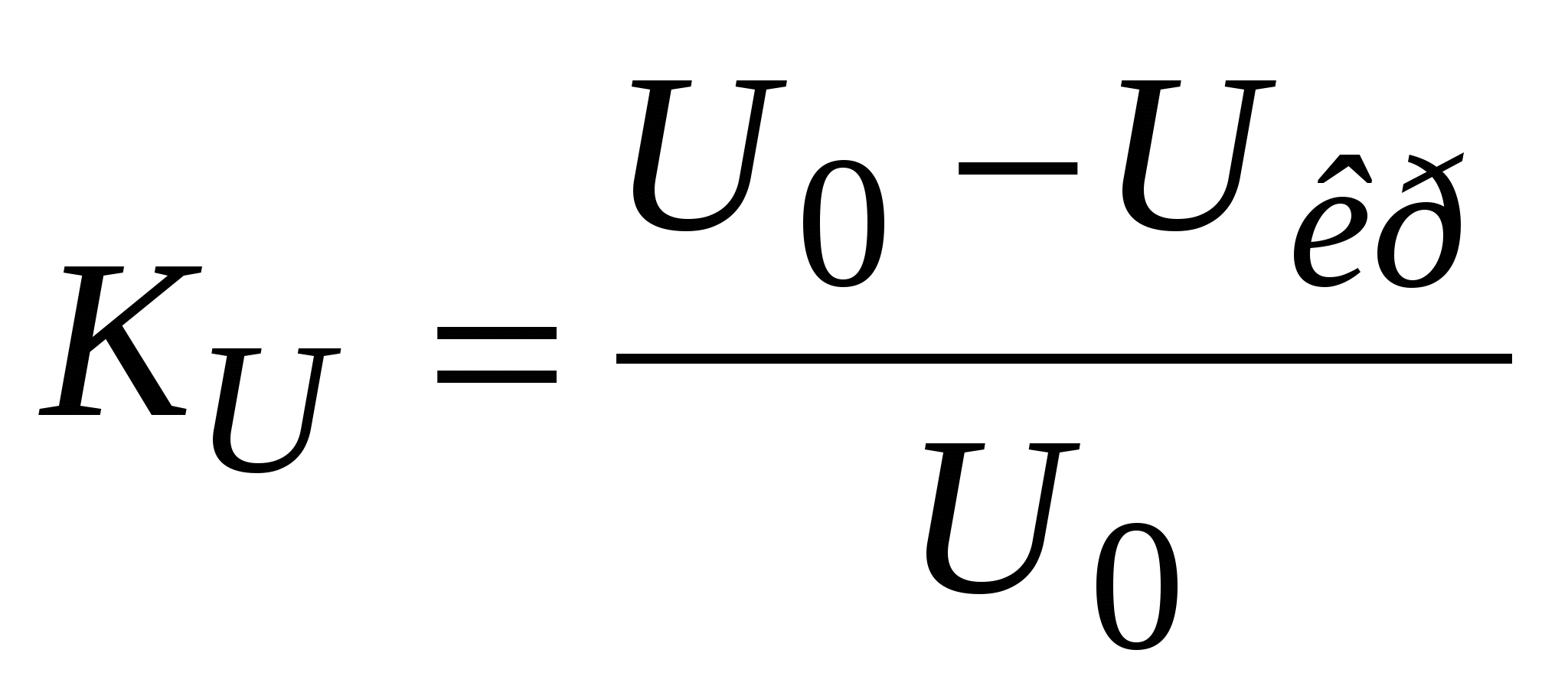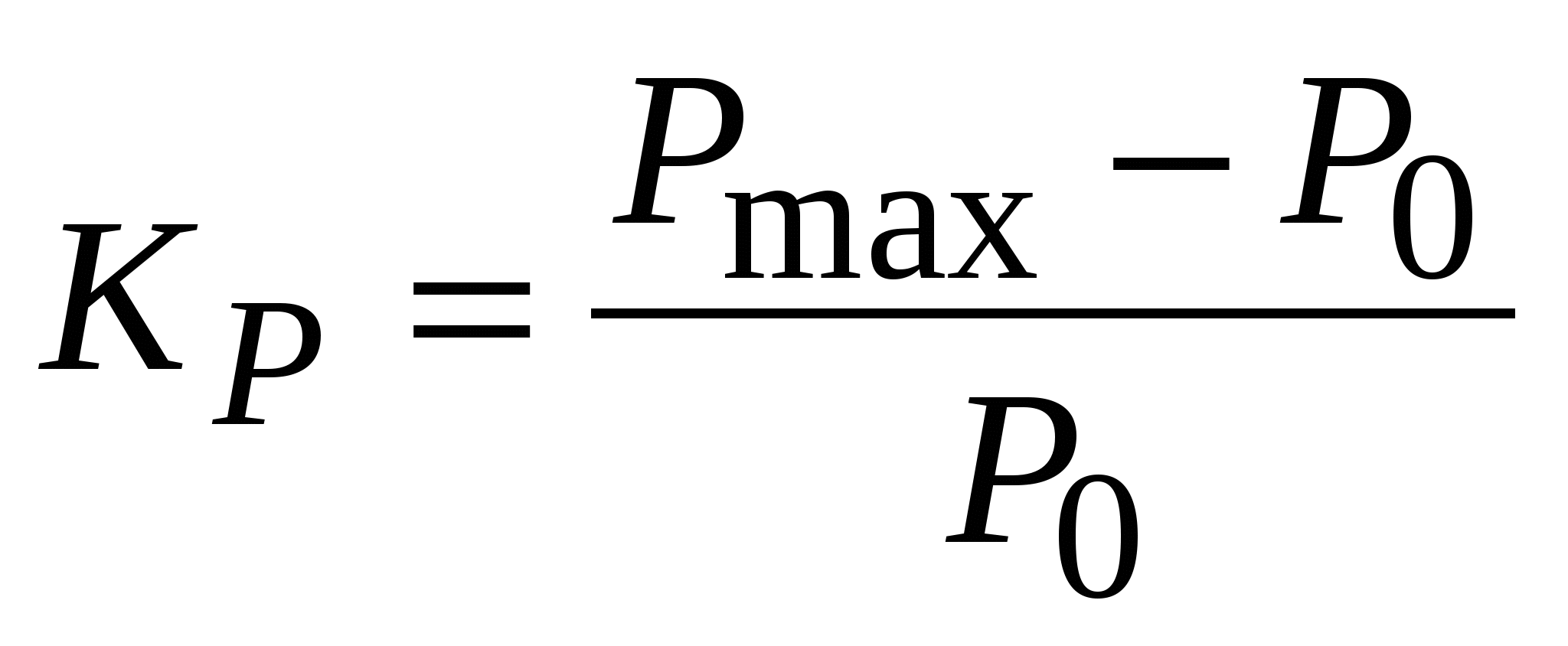Запас устойчивости электропередачи, связывающей станцию с шинами энергосистемы, должен быть не менее 20% в нормальном режиме и 8% в кратковременном послеаварийном [Л.5, с. 177].

Задачи анализа статической устойчивости.

1. Расчёт параметров предельных режимов (предельной передаваемой мощности по линиям, критического напряжения узловых точек системы, питающих нагрузку, и т.д.).

2. Определение значений коэффициентов запаса. Вместе с коэффициентами запаса по напряжению и мощности могут вычисляться коэффициенты запаса по настроечным параметрам АРВ:

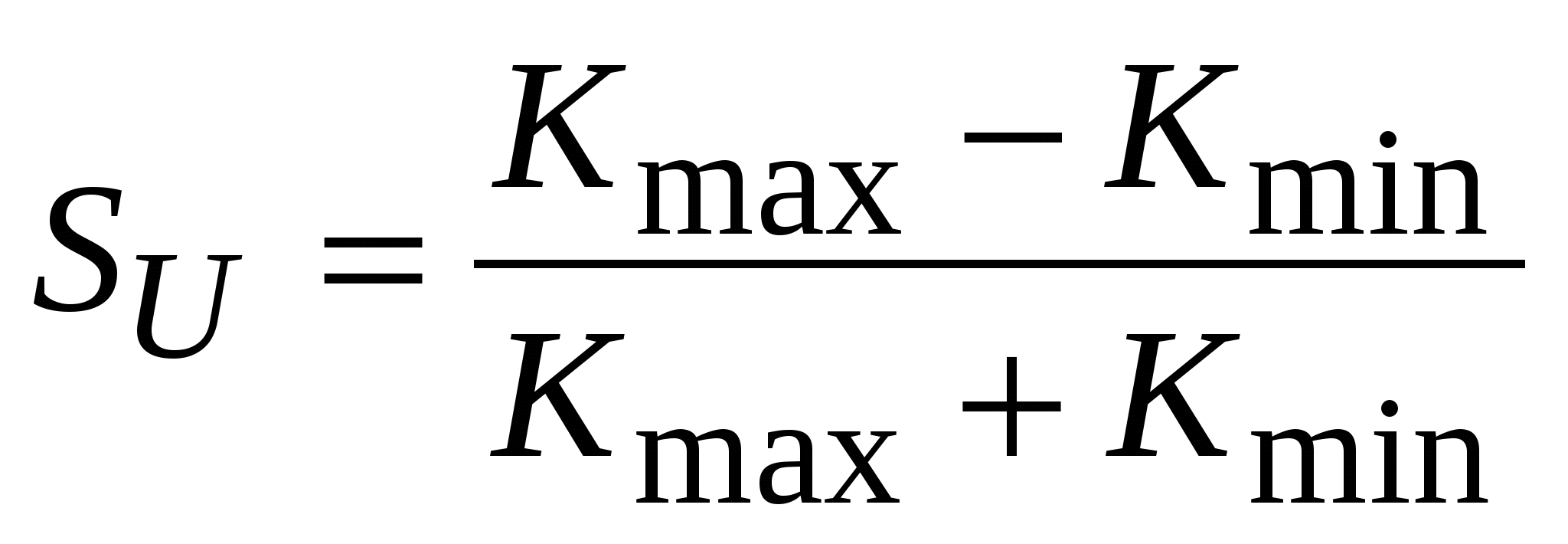, где К_maxи К_min– максимальное и минимальное значения настроечных параметров, соответствующих границе области статической устойчивости.

3. Выбор мероприятий по повышению статической устойчивости энергосистем или обеспечению заданной пропускной способности передачи.

4. Разработка требований, направленных на улучшение устойчивости систем. Выбирается настройка АРВ, обеспечивающая требуемую точность поддержания напряжения.

Задачи анализа динамической устойчивости.

Эти задачи связаны с переходом системы от одного установившегося режима к другому.

Результатами расчёта динамической устойчивости являются:

1. Предельное время отключения расчётного вида КЗ в наиболее опасных точках системы.

2. Паузы систем АПВ, установленных на различных элементах электрической системы.

3. Параметры систем автоматического ввода резерва (АВР).