Первая теорема Ляпунова об устойчивости (А.М. Ляпунов, 1892 г.) в терминах функций Хана.

Если для системы (2.1.1)÷(2.1.3) существует функция Ляпунова 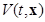, непрерывно дифференцируемая по t и x в области 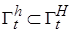и такая, что для некоторой функции Хана 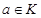и t , xиз области :

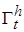1) ;

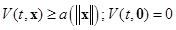2) ,

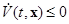то тривиальное решение системы (2.1.1) устойчиво (по Ляпунову при ).■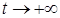

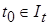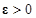Доказательство. Пусть заданы произвольные и . Так как V непрерывна и 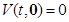, то найдется 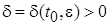, такое, что

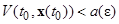для всех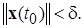

Рассмотрим все решения с начальными данными :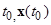

,

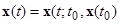начинающиеся из 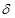-окрестности . Используя условие (2) теоремы, для любых 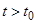и 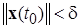получаем

.

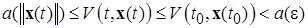Поскольку 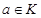, то заключаем, что 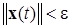.□ Теорема доказана.

Замечания.

1. Сравнение приведенных двух вариантов формулировок и доказательств первой теоремы Ляпунова позволяет оценить компактность и лаконичность современного языка математической теории систем.

2. В дальнейшем изложении ограничимся кратким обзором некоторых результатов второго метода Ляпунова , как правило, комментируя их, но не сопровождая подробными доказательствами, которые можно найти в литературных источниках, список которых приведен в конце изложения всего материала. ■

Вторая теорема Ляпунова об асимптотической устойчивости (А.М. Ляпунов, 1892)

Пусть дана приведенная система (2.1.1) ÷ (2.1.3) и пусть в некоторой области 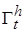найдется функция Ляпунова 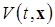, непрерывно дифференцируемая в этой области, и такая, что найдутся три не зависящие от времени положительно определенные функции Ляпунова

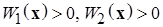и

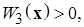
такие, что выполняются следующие соотношения (в области ):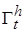

1) 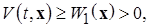т. е. 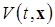– положительно определенная;

2) 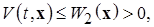т. е. 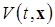допускает сильный БМВП при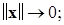

3) полная производная по времени в силу системы (2.1.1) 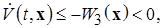т. е. 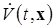– отрицательно определенная в .

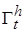Тогда тривиальное решение приведенной системы (2.1.1) асимптотически устойчиво при 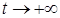с областью аттрактивности (с областью притяжения) . ■

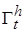Замечание. Не будем рассматривать, как условились, полное доказательство этой теоремы, а ограничимся некоторыми комментариями, опирающимися на геометрический смысл полной производной (см. п. 1.7).

Сначала заметим, что из первого и третьего условий теоремы следует устойчивость по Ляпунову тривиального решения в силу первой теоремы Ляпунова. Но, в силу наличия третьего условия – отрицательной определенности полной производной, произвольное решение 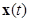не может «застаиваться» ни в какой 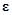-окрестности, в которой сохраняется отрицательность производной, а наличие БМВП при 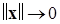(второе условие) позволяет этой 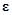-окрестности быть сколь угодно малой. Поэтому отрицательность производной будет «заставлять» решение 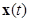переходить во все «меньшие» и «меньшие» 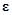-окрестности, пока решение 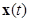не «сольется» с началом координат 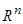при 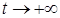, что и означает асимптотическую устойчивость тривиального решения системы.

Причем такое поведение характерно для каждого решения, начинающегося в области 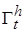, в которой выполняются все три условия теоремы, а, следовательно, эта область и является областью притяжения тривиального решения системы (2.1.1).■

Определение (неустойчивости по Ляпунову). Тривиальное решение (положение равновесия) 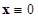называется неустойчивым по Ляпунову, если для некоторых 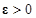, 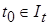и любого 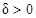существует (хотя бы одно) решение 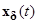и момент времени 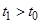такие, что

.■

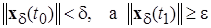Третья теорема Ляпунова о неустойчивости (А.М. Ляпунов, 1892)

Пусть дана приведенная система (2.1.1)÷(2.1.3) и пусть для нее найдется непрерывно дифференцируемая по t и x в некоторой области 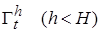функция Ляпунова 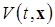, допускающая БМВП при 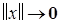и обладающая знакоопределенной производной 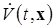, вычисленной в силу системы.

Если при некотором 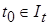в любой окрестности 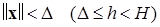найдется точка 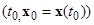, для которой знак функции V одинаков со знаком производной 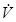, т.е. такая, что

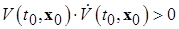, (2.1.10)

то тривиальное решение системы (2.1.1) неустойчиво по Ляпунову. ■

Без доказательства.