Первая теорема Ляпунова об устойчивости (А.М. Ляпунов, 1892).

Пусть найдется функция Ляпунова 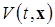, непрерывно дифференцируемая по t, x в некоторой области 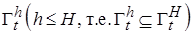и такая, что в этой области 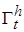она:

1) 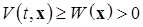(2.1.4)

где 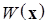– некоторая не зависящая от времени положительно определенная функция Ляпунова; 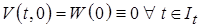, т. е. 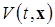– положительно определенная функция Ляпунова в ;

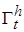2) ее полная производная, вычисленная в силу системы (2.1.1)

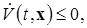(2.1.5)

т.е. 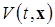– знакопостоянная отрицательная функция Ляпунова в области .

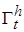Тогда тривиальное решение 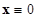, приведенной системы (2.1.1)÷(2.1.3) устойчиво по Ляпунову при 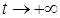(в смысле данного в п. 1.2 определения устойчивости по Ляпунову при 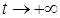тривиального решения системы).■

В качестве примера рассмотрим подробно доказательство этой теоремы, основанное, как и все доказательства результатов второго метода Ляпунова, на исследовании поведения функции (или функций) Ляпунова и ее полной производной, вычисленной в силу системы, т.е. на решениях системы, или, как говорят, вдоль решений системы. При этом целью доказательства является, опираясь на язык 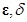- окрестностей, показать, что из условий теоремы следует свойство тривиального решения, подпадающее под «юрисдикцию» соответствующего определения 1’ устойчивости по Ляпунову при 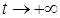(п. 1.2).

Доказательство [1]. На основании условия (2.1.4) теоремы рассмотрим в 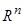по любом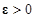у сферу :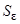

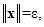
целиком лежащую в области 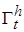непрерывной дифференцируемости данной функции Ляпунова 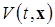(2.1.4), т.е.

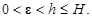
Так как сфера 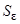- компактное множество и функция 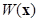непрерывна и положительна на 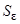, то, в силу теоремы Вейерштрасса, точная нижняя грань этой функции достигается в некоторой точке

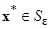
и, следовательно,

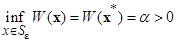(2.1.6)

Пусть теперь 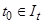произвольно. Функция 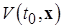(при фиксированном времени) по условиям теоремы непрерывна по x и 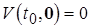. Следовательно, существует окрестность

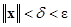
такая, что выполняется неравенство

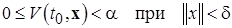(2.1.7)

Рассмотрим любое нетривиальное решение системы (2.1.1)

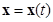. (2.1.8)

с начальным условием

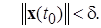
Докажем, что траектория этого решения целиком остается внутри сферы 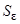, т.е.

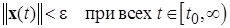. (2.1.9)

В силу выбора 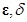- окрестностей при 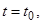уже имеем

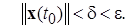
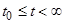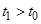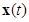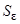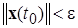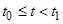Докажем справедливость предположения (2.1.9) «от противного»: пусть неравенство (2.1.9) выполнено не для всех и - точка первого выхода решения на границу сферы , т.е. при и 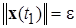. Исследуем поведение функции Ляпунова (2.1.4) вдоль решения 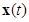, обозначая:

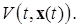
Так как в силу условия (2.15) теоремы

,

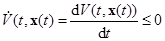то функция 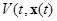невозрастающая. Следовательно, учитывая формулы (2.1.7) и (2.1.6), имеем:

,

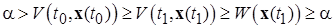т.е. получили противоречие, что и доказывает справедливость неравенства (2.1.9) для всех .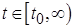

Мы исчерпали все условия теоремы, следовательно, можно подводить итоги доказательства, а именно, произвольно взятое решение 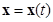при любом конечном 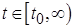остается внутри сферы 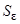, а значит так как 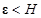, это решение бесконечно продолжимо вправо, т.е. определено при всех 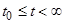, причем оно навсегда остается внутри 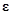-окрестности, т.е.

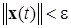при всех ,

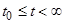если только оно начинается внутри 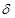-окрестности, т.е.

.

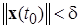Таким образом, согласно определению 1’ устойчивости по Ляпунову (см. п. 1.2) тривиальное решение 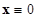системы (2.1.1) устойчиво по Ляпунову при 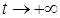, что и требовалось доказать. □

Следствие. Если выполняются условия теоремы для системы (2.1.1)÷(2.1.3), то все ее решения 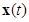, начинающиеся внутри некоторой «достаточно малой» 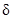-окрестности

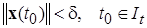
бесконечно продолжимы вправо и ограничены на всем полубесконечном интервале .■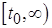

Мы рассмотрели один из многих вариантов подробного доказательства первой теоремы Ляпунова, близкого по форме к классическим рассуждениям, характерным для самого основателя метода функций Ляпунова, доказавшего ее в 1892 г. В качестве другого примера доказательства этой теоремы приведем более компактное доказательство и для этого прибегнем к рассмотренным выше (см. п. 1.5.1) функциям Хана вида .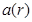

Запишем формулировку в терминах функций Хана [5].