Теорема (о свойствах вещественной квадратичной формы).

Пусть дана вещественная квадратичная форма

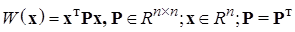
Тогда имеет место следующее утверждение:

а) 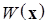– функция Ляпунова, допускающая бесконечный предел в целом.

б) имеет место так называемый критерий Сильвестра.

Критерий Сильвестра.

1. Квадратичная форма 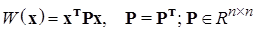является положительно определенной тогда и только тогда, когда все главные последовательные диагональные миноры матрицы Р квадратичной формы строго положительны, т. е. для матрицы вида

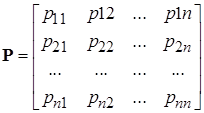
имеют место следующие неравенства:

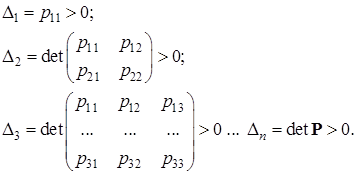(1.5.4)

2. Квадратичная форма 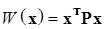является отрицательно определенной функцией Ляпунова тогда и только тогда, когда главные последовательные диагональные миноры матрицы 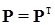имеют перемежающиеся знаки, а именно:

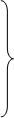
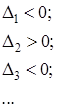. (1.5.5)

(в) Вещественная симметричная матрица 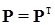, 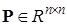всегда имеет только вещественные собственные значения - корни характеристического многочлена матрицы вида:

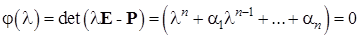(1.5.6)

где 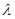- формальная скалярная переменная, Е – единичная матрица.

(г) Для любой квадратичной формы

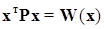
имеет место следующая двусторонняя оценка:

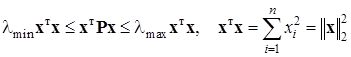(1.5.7)

где 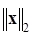— векторная евклидова норма ( 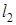— норма) 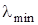, 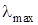— соответственно, наименьшее и наибольшее собственные значения симметричной матрицы P (без доказательства).■

Замечание. Поскольку вещественная квадратичная форма однозначно определяется матрицей 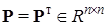, то зачастую пишут 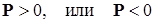, имея ввиду, что матрица P определяет положительно определенную или отрицательно определенную вещественную квадратичную форму.■