Приведенная (по Ляпунову) система
В математических методах исследования устойчивости систем нелинейных и нестационарных дифференциальных уравнений с помощью второго (или прямого) метода Ляпунова имеют дело только с системами, допускающими тривиальное решение. Рассмотрим формальную процедуру приведения задачи исследования свойств устойчивости произвольного фиксированного решения системы к задаче исследования тривиального решения эквивалентной системы, допускающей тривиальное решение. Такую эквивалентную систему и будем называть (вслед за Ляпуновым) приведенной.
Пусть дана конечномерная гладкая динамическая система с непрерывным временем вида
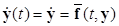 (1.3.1)
(1.3.1)
и дано некоторое ее фиксированное решение 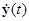 , подлежащее исследованию.
, подлежащее исследованию.
Введем обозначение новой переменной
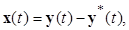
где 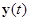 - любое решение системы (1.3.1), т.е.
- любое решение системы (1.3.1), т.е. 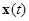 есть отклонение произвольного решения
есть отклонение произвольного решения 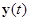 от решения
от решения 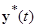 . Тогда, так как
. Тогда, так как
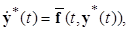
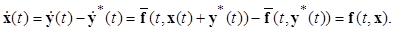
Получим дифференциальное уравнение для отклонений вида
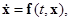 (1.3.2)
(1.3.2)
где обозначено:
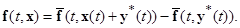
Получили некоторую «новую» систему (1.3.2), эквивалентную «старой» системе (1.3.1), путем исключения из «старой» системы (1.3.1) некоторого решения 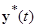 , которое считаем известным и устойчивость которого подлежит исследованию. Очевидно, что система (1.3.2) допускает (в силу построения) тривиальное решение
, которое считаем известным и устойчивость которого подлежит исследованию. Очевидно, что система (1.3.2) допускает (в силу построения) тривиальное решение 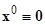 , что легко проверить его подстановкой.
, что легко проверить его подстановкой.
Таким образом, привели задачу исследования устойчивости произвольного известного решения 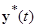 системы (1.3.1) к задаче исследования устойчивости тривиального решения (положения равновесия)
системы (1.3.1) к задаче исследования устойчивости тривиального решения (положения равновесия) 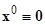 так называемой «приведенной» системы (1.3.2) (по Ляпунову она называется также системой уравнений возмущенного движения, а решение
так называемой «приведенной» системы (1.3.2) (по Ляпунову она называется также системой уравнений возмущенного движения, а решение 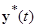 - невозмущенным движением).
- невозмущенным движением).
Функции Ляпунова
Пусть дана приведенная система
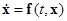 (1.4.1)
(1.4.1)
с областью определения fвида
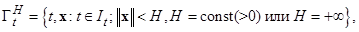 (1.4.2)
(1.4.2)
причем fудовлетворяет свойствам (1.1.9), т.е. непрерывна по t и xи непрерывно дифференцируема по x.Кроме того, введем дополнительное ограничительное условие для f:
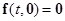 (1.4.3)
(1.4.3)
т.е. система (1.4.1) допускает тривиальное решение.
Определение 1.Скалярная вещественная функция векторного аргумента xи времени t вида
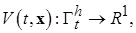 (1.4.4)
(1.4.4)
определенная в некоторой области
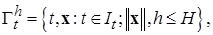 (1.4.5)
(1.4.5)
такой, что 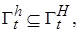 называется функцией Ляпунова (ФЛ) для системы(1.4.1) в области
называется функцией Ляпунова (ФЛ) для системы(1.4.1) в области 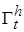 (короче, функцией Ляпунова) если она удовлетворяет следующим требованиям (свойствам):
(короче, функцией Ляпунова) если она удовлетворяет следующим требованиям (свойствам):
а) 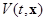 - скалярная вещественная функция (скалярную функцию векторных аргументов часто называют функционалом);
- скалярная вещественная функция (скалярную функцию векторных аргументов часто называют функционалом);
б) 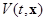 - непрерывная функция по t и x;
- непрерывная функция по t и x;
в) 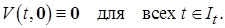 ■
■
Определение 2. Функция Ляпунова 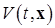 называется знакопостояннойв области
называется знакопостояннойв области 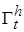 , а именно:
, а именно:
(а) знакопостоянной положительной (знакоположительной), если 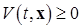 в области
в области 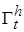 ;
;
(б) знакопостоянной отрицательной (знакоотрицательной), если 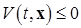 в области
в области 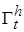 .■
.■
Определение 3. Функция Ляпунова 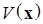 , не зависящая от времени, называется знакоопределенной в области
, не зависящая от времени, называется знакоопределенной в области 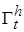 , а именно:
, а именно:
(а) положительно определенной (определенно положительной) в области 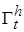 , если
, если 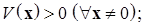
(б) отрицательно определенными (определенно отрицательной) в области 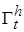 , если
, если 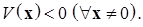 ■
■
Определение 4. Функция Ляпунова вида 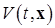 , зависящая от времени, называется знакоопределенной в области
, зависящая от времени, называется знакоопределенной в области 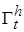 , а именно:
, а именно:
а) положительно определенной в области 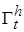 , если выполнено неравенство:
, если выполнено неравенство:
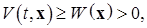
где 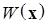 – не зависящая от времени положительно определенная функция Ляпунова, удовлетворяющая определению 3, т.е.
– не зависящая от времени положительно определенная функция Ляпунова, удовлетворяющая определению 3, т.е. 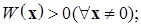
б) отрицательно определенной в области 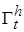 , если выполнено неравенство
, если выполнено неравенство
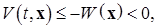
где 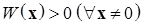 .■
.■
Таким образом, для зависящих от времени знакоопределенных функций Ляпунова в области 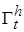 выполняется неравенство
выполняется неравенство
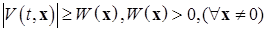 , (1.4.6)
, (1.4.6)
где 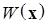 - не зависящая от времени положительно определенная функция Ляпунова.
- не зависящая от времени положительно определенная функция Ляпунова.
Полезное правило. Согласно определению 4, критерием, определяющим свойство положительной определенности функции Ляпунова, зависящей от времени, является некоторая не зависящая от времени положительно определенная функция 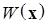 , которую необходимо найти. Укажем один из приемов ее построения.
, которую необходимо найти. Укажем один из приемов ее построения.
Пусть дана зависящая от времени функция Ляпунова 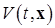 в области
в области 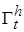 . Если может быть построена в той же в области
. Если может быть построена в той же в области 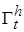 не зависимая от времени функция вида
не зависимая от времени функция вида
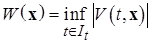 , (1.4.7)
, (1.4.7)
где inf (инфинум) – точная нижняя грань множества всех значений 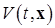 по
по 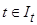 (а точная верхняя грань обозначается как sup (супремум), то ее можно взять в качестве
(а точная верхняя грань обозначается как sup (супремум), то ее можно взять в качестве 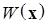 в определении 4 для исследования знакоопределенности функции
в определении 4 для исследования знакоопределенности функции 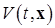 , а именно, из (1.4.7) очевидно, что:
, а именно, из (1.4.7) очевидно, что:
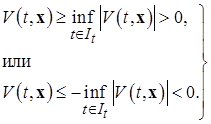 (1.4.8)
(1.4.8)
Пример применения полезного правила. Рассмотрим в 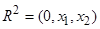 функцию Ляпунова вида
функцию Ляпунова вида
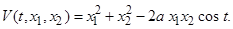 (1.4.9)
(1.4.9)
1. При 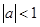 функция (1.4.9) является положительно определенной в
функция (1.4.9) является положительно определенной в  , так как
, так как
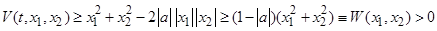 при
при 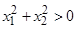 и
и

Действительно, из 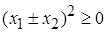 следует
следует 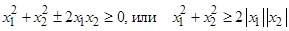 . Тогда, усиливая неравенство, получим
. Тогда, усиливая неравенство, получим
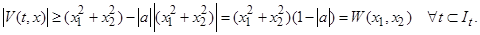
Очевидно, что здесь для функции (1.4.9) найдена не зависящая от времени функция Ляпунова 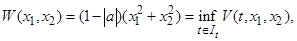 такая что при
такая что при 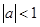
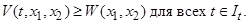
2. При 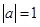 функция
функция 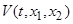 лишь знакопостоянная положительная.□
лишь знакопостоянная положительная.□
Дата добавления: 2016-11-02; просмотров: 820;
