Геометрическая интерпретация знакоопределенной функции.
Пусть дана положительно определенная функция Ляпунова 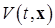 - и найдена
- и найдена 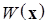 , такая, что
, такая, что 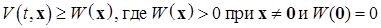 .
.
Предположим, что поверхности уровня вида
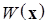 =Сi (Сi=const,
=Сi (Сi=const, 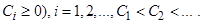 (1.4.10)
(1.4.10)
в пространстве 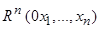 представляют собой семейство непрерывных замкнутых поверхностей, окружающих начало координат 0 и монотонно расширяющихся при росте параметра
представляют собой семейство непрерывных замкнутых поверхностей, окружающих начало координат 0 и монотонно расширяющихся при росте параметра 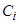 (рисунок 2). Тогда очевидно, что каждая поверхность уровня вида
(рисунок 2). Тогда очевидно, что каждая поверхность уровня вида
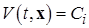 (1.4.11)
(1.4.11)
для любого 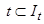 будет целиком расположена внутри соответствующей поверхности уровня
будет целиком расположена внутри соответствующей поверхности уровня 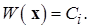 (см. рисунок 2).
(см. рисунок 2).
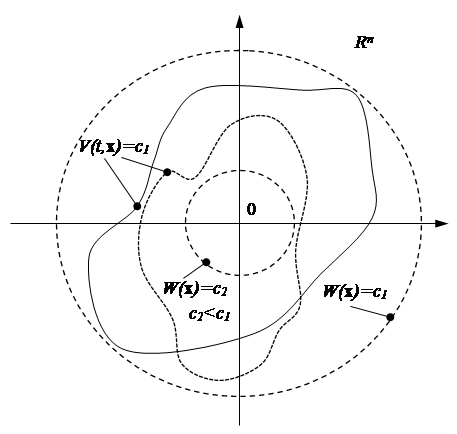
Рисунок 2
Определение 5. Функция Ляпунова вида 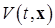 называется функцией, допускающей бесконечно малый высший предел (БМВП) при
называется функцией, допускающей бесконечно малый высший предел (БМВП) при 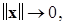 если существует предел
если существует предел 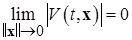 равномерный на
равномерный на 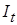 , т.е. по
, т.е. по 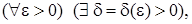 выбор которого не зависит от выбора
выбор которого не зависит от выбора 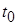 , такое, что при
, такое, что при 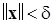 будет
будет 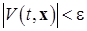 (начиная с некоторого
(начиная с некоторого 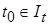 ).■
).■
Определение 6.Функция Ляпунова вида 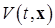 называется функцией, допускающей бесконечно большой низший предел (ББНП) при
называется функцией, допускающей бесконечно большой низший предел (ББНП) при 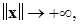 если существует предельное соотношение
если существует предельное соотношение 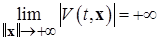 , равномерное на
, равномерное на 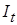 , т. е. по любому числу
, т. е. по любому числу 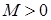 найдется другое число
найдется другое число 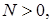 выбор которого не зависит от выбора
выбор которого не зависит от выбора 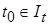 , такое, что при
, такое, что при 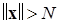
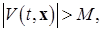 начиная с некоторого
начиная с некоторого 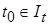 .■
.■
Замечание. Корректное определение функции Ляпунова, допускающей ББНП при 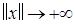 , должно опираться на систему, областью определения
, должно опираться на систему, областью определения 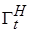 которой должно служить все
которой должно служить все 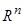 , т.е.:
, т.е.:
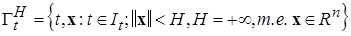 . (1.4.12)
. (1.4.12)
При этом говорят, что система определена на всем 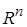 .■
.■
Определение 7. Функция Ляпунова 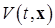 , допускающая БМВП при
, допускающая БМВП при 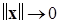 и ББНП при
и ББНП при 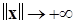 называется функцией Ляпунова, допускающей бесконечный предел в целом (глобальный бесконечный предел). ■
называется функцией Ляпунова, допускающей бесконечный предел в целом (глобальный бесконечный предел). ■
Определение 8. Функция Ляпунова 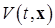 называется функцией, допускающей сильный БМВП при
называется функцией, допускающей сильный БМВП при 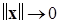 , если найдется независимая от времени положительно определенная функция Ляпунова
, если найдется независимая от времени положительно определенная функция Ляпунова 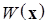 , такая, что имеет место неравенство:
, такая, что имеет место неравенство:
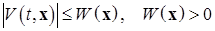
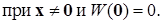 (1.4.13)
(1.4.13)
Замечание. Очевидно, что функция Ляпунова, не зависящая от времени, всегда имеет сильный БМВП при 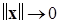 (в силу того, что функция Ляпунова непрерывна по х и
(в силу того, что функция Ляпунова непрерывна по х и 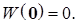 ■
■
Замечание.Для функции Ляпунова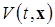 , зависящей от времени, можно практиковать такую двухстороннюю запись:
, зависящей от времени, можно практиковать такую двухстороннюю запись:
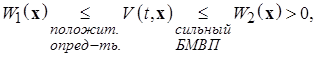 (1.4.14)
(1.4.14)
где 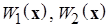 – положительно определенные не зависящие от времени функции Ляпунова.
– положительно определенные не зависящие от времени функции Ляпунова.
Такая запись (1.4.14) означает, что функция Ляпунова 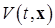 - положительно определенная и допускает сильный БМВП при
- положительно определенная и допускает сильный БМВП при 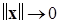 .■
.■
Дата добавления: 2016-11-02; просмотров: 919;
