Геометрический смысл полной производной по времени функции Ляпунова, вычисленной в силу приведенной системы

Пусть (для определенности) дана положительно определенная функция Ляпунова 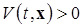. Знание ее производной в силу системы (1.6.1) позволяет наглядно выяснить характер движения изображающей точки вдоль интегральной кривой (решения) системы.

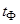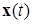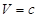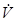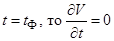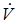Действительно, пусть в некоторый фиксированный момент времени изображающая точка М занимает некоторое положение на кривой (решении) системы (1.6.1). Построим поверхность (с – положительное число), проходящую через точку М. Затем по формуле (1.6.4) вычислим полную производную функции V в этой точке. Так как , и будет равна скалярному произведению вектор-функций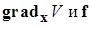

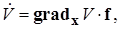(1.7.1)

причем напомним, что вектор-функция fопределяет вектор скорости движения изображающей точки вдоль решения 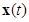системы. Рассмотрим три возможных случая.

Рис. 6, а

Рис. 6, б

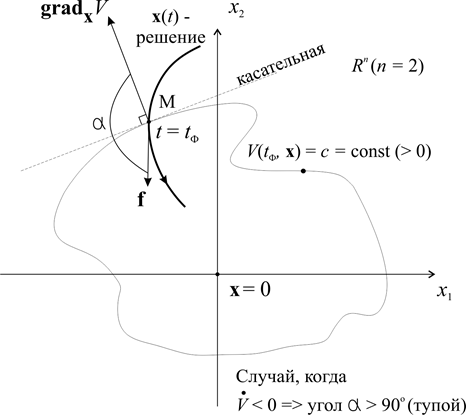
1. Пусть в данном положении точки М производная 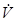отрицательна

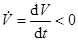
т.е. функция V убывает на решении 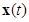системы (см. рисунок 6,а).

Известно, что вектор 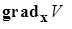направлен по нормали к поверхности 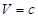в точке М в сторону возрастания функции V, т.е.во внешнюю часть поверхности V=с, если функция Ляпунова V положительно определенная (и внутрь поверхности 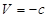, если V отрицательно определенная), а вектор-функция fскорости движения точки М касателен к кривой решения в точке М.

Таким образом, отрицательность 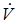- скалярного произведения (1.7.1) векторов 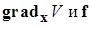означает, что угол между ними тупой, и так как вектор 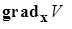направлен по внешней нормали к поверхности 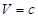в точке М , то вектор скорости fточки М направлен внутрь этой поверхности. А это означает, что траектория изображающей точки М (интегральная кривая, решение системы) пересекает поверхность 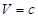снаружи вовнутрь (см. рисунок 6,а).

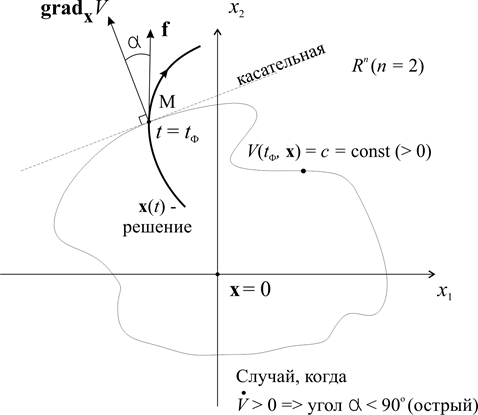
2. Пусть в данном положении точки М 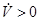, т.е. функция V возрастает на решении системы (см. рисунок 6,б). Положительность 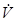- скалярного произведения (1.7.1) векторов 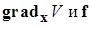означает, что угол между ними острый, и, следовательно, траектория изображающей точки М пересекает поверхность 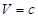изнутри наружу (см. рисунок 6,б).

3. Пусть в данном положении точки М производная 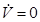, т.е. скалярное произведение векторов 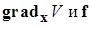равно нулю, угол между этими векторами - прямой, и следовательно, траектория изображающей точки М касается поверхности 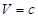(в частности, она может целиком лежать на этой поверхности).

Замечание. Главный идейный смысл второго, или, как его еще называют, прямого метода Ляпунова, состоит в том, что свойства устойчивости тривиального решения приведенной по Ляпунову системы, или, что то же, системы возмущенного движения, изучаются по поведению полной производной по времени функции Ляпунова, вычисленной в силу системы (говорят, вдоль решений системы уравнений возмущенного движения), причем сами решения остаются неизвестными, а их производные заменяются известными правыми частями 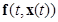, т.е. второй метод Ляпунова является косвенным методом исследования свойств устойчивости решений приведенной системы. ■