Математическая модель динамической системы. Определение адаптивной системы

Будем рассматривать конечномерную нелинейную и нестационарную систему обыкновенных дифференциальных уравнений в непрерывном времени (говорят, динамическую систему, динамический объект или, короче, объект) вида:

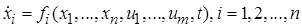, (1.1.1)

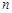-порядок системы, .

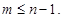Систему (1.1.1) для краткости будем записывать в виде векторного уравнения:

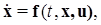(1.1.2)

где 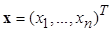- вектор состояния, 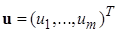- вектор управления, t - время (вещественная переменная),

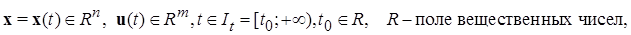
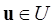- множество допустимых управлений - вектор-функции u, 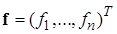- правые части дифференциальных уравнений (1.1.1) или (1.1.2), 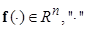, означает неназванные аргументы.

Область[1] определения вектор-функции fправых частей дифференциальных уравнений (1.1.1) или (1.1.2) имеет следующий вид:

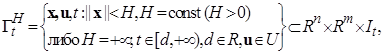(1.1.3)

где знак «×» означает декартово произведение множеств,

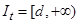- множество моментов времени (вещественная полуось), 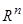- -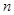мерное линейное (афинное) пространство над полем .

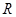В 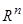можно построить какую либо норму («длину» вектора), например, векторную евклидову норму вида 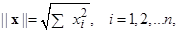тогда пара { 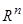, ||·||},называется линейным нормированным пространством (над полем R).

Вектор-функция 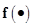в области 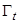обладает следующими свойствами:

(а) f - непрерывна по всем аргументам ;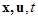

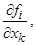
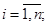
(б) f - имеет непрерывные частные производные вида 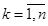, (1.1.4) ограниченные равномерно по 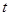на любом компактном подмно-

жестве из области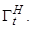

Условия (1.1.4) обеспечивают однозначную разрешимость системы дифференциальных уравнений (1.1.1) или (1.1.2) для любой тройки 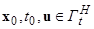,т.е для любой точки 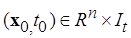и некоторого управления 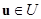существует единственное решение системы дифференциальных уравнений (1.1.2) вида 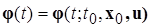, определённое на некотором промежутке 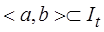, 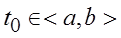и удовлетворяющее тождеству:

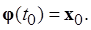(1.1.5)

Пара 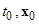называется начальными данными решения 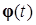, тождество (1.1.5) называется начальным условием решения 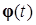, а само решение называется решением задачи Коши.

Таким образом, условия (1.1.4) обеспечивает существование и единственность решения, проходящего через любую точку 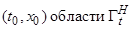с некоторым управлением u. А это означает, что для системы дифференциальных уравнений (1.1.2) имеет место следующая эквивалентность:

условия (1.1.4) для 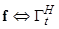-область единственности.

Определение. Система дифференциальных уравнений (1.1.1) или (1.1.2) определяет так называемую конечномерную гладкую динамическую систему с непрерывным временем. Это наиболее общая (и общеупотребительная) математическая модель нелинейной и нестационарной динамической системы, которую рассматривает современная математическая теория систем управления. ■

Определение.Динамическая система (1.1.2) называется системой с обратной связью, если управление u есть функция состояния 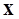и времени:

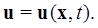
Тогда

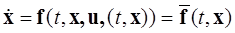(1.1.6)

называется системой с обратной связью (по состоянию), или замкнутой системой (по состоянию). ■

Замечание. Отметим, что в системе с обратной связью по состоянию (1.1.6) из правых частей исключено управление и они зависят только от аргументов 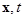, поэтому при дальнейшем изложении методов теории устойчивости систем управления будем описывать систему векторным уравнением 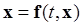, опуская черточку над fв уравнении (1.1.6) и аргумент uв уравнении (1.1.2).■

Определение. Решением системы

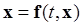(1.1.7)

называется функция 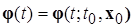, обладающая следующими свойствами:

(а) 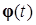- определена, непрерывна и непрерывно дифференцируема по 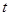на некотором промежутке 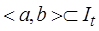, включающем точку t₀;

(б) точки 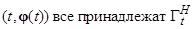- области определения системы (1.1.7) вида (опускаем аргумент u):

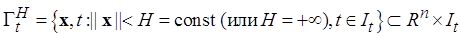; (1.1.8)

(в) 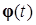удовлетворяет уравнению (1.1.7):

■

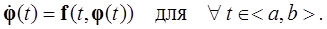Определение. Решение 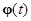системы (1.1.7) называется бесконечно продолжимым (продолжаемым) вправо, если оно определено на всем полубесконечном интервале времени . ■

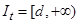В теории дифференциальных уравнений имеет место следующая теорема.

Теорема (о свойствах продолжимости решений дифференциальных систем)

Пусть дана система (1.1.7)

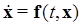
и пусть область 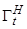существования f вида (1.1.8) есть область единственности, то есть правые части f удовлетворяют свойствам:

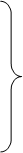а) f - непрерывно по ;

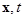б) f - непрерывно дифференцируема по x и 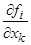- (1.1.9)

ограничены равномерно по 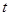на любом компактном

подмножестве из .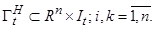

Тогда все решения системы (1.1.7) обладают следующими взаимоисключаемыми свойствами:

(а) либо все решения 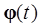бесконечно продолжимы вправо;

(б) либо все решения 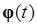- существуют на ограниченном интервале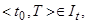 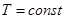, 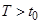и имеет место следующие предельное соотношение: 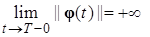, то есть при бесконечном приближении к правому концу 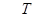интервала слева решение уходит на 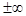(по норме) ■.

В дальнейшем будем обозначать решение 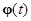системы (1.1.7) той же буквой :

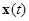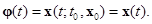
Определение адаптивной системы. Формулировка задачи адаптивного управления (на содержательном уровне).В адаптивном управлении используют следующую математическую модель динамической системы (объекта):

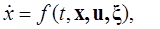(1.1.10)

Пусть модель (1.1.10) задана в области (1.1.3) и f(·) удовлетворяет условиям (1.1.4).

Эта модель является иной записью уравнения (1.1.2) 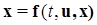, когда в описании системы подчеркивают то, что она не может быть полностью определена, то есть в правых частях ее дифференциальных уравнений имеются неизвестные параметры и (или) функции. Эти неизвестные свойства правых частей «вносят» в некоторую неизвестную вектор-функцию вида

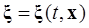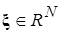, , (1.1.11)

где 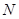- любое положительное целое число.

Определение. Динамическая система (объект) (1.1.10) называется системой (объектом) с параметрической неопределенностью если 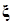- постоянный (числовой) вектор или вектор-функция времени .

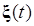Динамическая система (объект) (1.1.10) называется системой (объектом) с функционально-параметрической неопределённостью, если вектор – функция 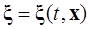зависит, вдобавок, от состояния■.

Итак, 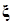- N-мерная вектор-функция неизвестных параметров и функций системы (1.1.10), причем N не ограничено размерностью n системы.

Вектор функция 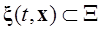принадлежит множеству неизвестных функций 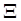, называемому множеством неопределенности, или классом адаптивности системы (объекта) (1.1.10).

Таким образом, имеем дело с множеством объектов или систем вида (1.1.10), характеризуемых классом адаптивности (неопределенности) 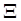. Говорят, что множество 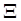определяет класс адаптивности (неопределенности) системы (1.1.10).

Замечание. Очевидно, что все аргументы 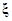должны принадлежать области определения системы (1.1.10). Полагаем так же, что N-вектор 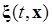не зависит от функции ■

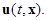Рассматривают следующие этапы построения адаптивного управления для системы (1.1.10):

1. Задают класс адаптивности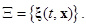

2. Формулируют цель адаптивного управления. Она, как правило, определяется некоторым целевым функционалом

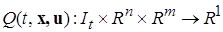, (1.1.12)

где Q - скалярная вещественная функция векторных аргументов 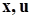и времени 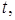и целевым неравенством вида

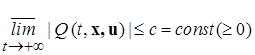, (1.1.13)

называемым целевым условием для целевого функционала (1.1.12).

3. Определяют закон адаптивного управления

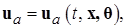(1.1.14)

где q- некоторая векторная функция настраиваемых параметров закона адаптивного управления 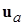. Отметим, что адаптивный закон (1.1.14) не должен зависеть от неизвестной вектор-функции 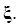Такое управление зачастую называется законом основного контура и подчеркивается, что оно строится по некоторым правилам, формулируемым вне задачи адаптивного управления.

4. Определяют правила настройки вектор-функции q, которые выражаются дифференциальным или алгебраическим уравнениями вида:

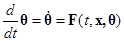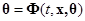, или (1.1.15)

Замечание. Вектор-функция q можетиметь размерность, вообще говоря, отличную от размерности N неизвестной вектор-функции x(t, x).■

Таким образом, приходят к системе (дифференциальных уравнений) вида:

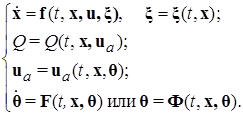(1.1.16)

Определение. Динамическая система (1.1.16) называется адаптивной системой, а подлежащие определению уравнения 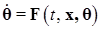или 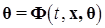называются алгоритмами параметрической настройки закона адаптивного управления 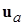(алгоритмами параметрической адаптации).■

Таким образом, задача адаптивного управления неопределенным объектом (1.1.10) может быть сформулирована следующим образом: найти (построить) закон адаптивного управления (закон основного контура) (1.1.14) не содержащий неизвестную вектор-функцию (1.1.11), и найти алгоритмы настройки (1.1.15) такие, чтобы обеспечивались ограниченность (по норме) всех решений адаптивной системы (1.1.16) и выполнение предельного целевого неравенства (1.1.13) во всем классе адаптивности (неопределенности) 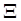объекта (1.1.10), т.е. для всех значений вектор-функции (1.1.11).■

Говорят также, что адаптивное управление (1.1.14) и алгоритмы настройки его параметров (1.1.15) обеспечивают асимптотически (в силу целевого неравенства (1.1.13)) нечувствительность (робастность) системы (1.1.16) к параметрическим рассогласованиям (возмущениям) вида (1.1.11).