Длина отрезка. Теорема существования измерения отрезков. Теорема единственности

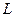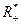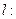
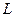
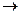
Пусть - множество всех отрезков, - множество всех положительных чисел. Говорят, что установлено измерение отрезков, если определено некоторое отображение 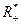, удовлетворяющее следующим аксиомам.

1). Если 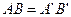, то равны их образы .

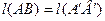2). Если точка B находится между А и C (A-B-С), то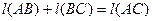

3). PQ- является единичным отрезком, если его образ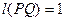

Определение 15.1.Отрезок PQ (или другой ему равный) удовлетворяющий аксиоме 3, называется линейной единицей или единичным отрезком.

Определение 15.2.Положительное число, соответствующее отрезку AB с указанием линейной единицей, называется мерой или длиной AB.

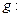
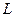
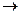
Теорема 15.3.(теорема существования)При любом выборе единичного отрезка РQ, существует отображение 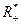, удовлетворяющее аксиома 1-3, причем 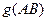есть число, полученное в результате измерения отрезка .

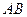Доказательство:

I) Существование отображения.

1) Пусть АВ – данный отрезок из множества L, РQ- единичный отрезок.

2) Рассмотрим процесс, с помощью которого определяется действительное положительное число 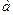, являющееся длиной отрезка АВ. Этот процесс называется измерением отрезка АВ. При измерении будем пользоваться представлением положительного числа в виде двоичной дроби 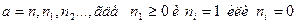_, (дробь, выражающая число а, может быть как конечной, так и бесконечной).

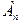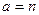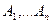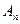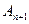3) На луче АВ отложим последовательно отрезки АА₁, А₁А₂, …, равные РQ. Если одна из точек – точка совпадает с точкой В, тогда . Если же ни одна из точек не совпадает с В, то по аксиоме Архимеда существуют такие две точки и , что .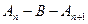

_· Пусть P₁ - середина А_nA_n+1 : А_n P₁= P₁А_n

Тогда при данном разбиении возможны случаи.

1). P₁≡В 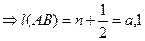(процесс измерения закончен);

2). А_n-B- 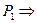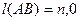или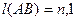

3). А_n-Р₁-В 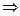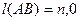или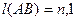

4). Рассмотрим середину 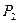того из отрезков А_n P₁ или P₁A_{n+1 ,} который содержит точку В. Пусть, например, В – точка отрезка А_n P₁ . Возможны три случая:

1) P₂≡В 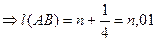(процесс измерения закончен);

2) А_n-B- 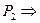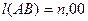или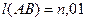

3) Р₂-В –Р₁ 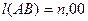или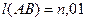

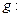
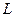
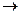
Продолжая этот процесс, приходим к определенному числу. Таким образом, построено конкретное отображение 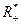, при котором каждому отрезку АВ ставится в соответствие число, полученное в результате его измерения.

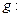
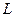
II). Докажем, что отображение , удовлетворяет аксиомам 1-3. Выполнение трех аксиом очевидно из построения данного отображения.

1. Выполнение аксиомы 3 очевидно, так как, применяя описанный выше процесс к измерению единичного отрезка 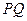, получаем число 1.

2. Выполнение аксиомы 1 также следует из процесса построения отображения.

3. Докажем выполнение 2 аксиомы. Для этого необходимы два утверждения:

1). Если 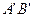< 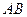то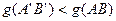

2). Пусть PQ=1, а EF – отрезок, в котором укладывается 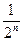- часть отрезка PQ укладывается 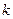раз, где 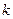- произвольное натуральное число. Тогда .

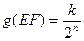Пусть А-В-С 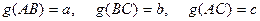. Докажем, 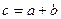(метод от противного).

Доказательство.

· Допустим, что 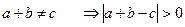. Выберем натуральное число 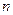, большее 1, так чтобы .

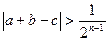· На луче ВА отложим последовательно отрезки 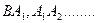равные отрезку РР_n = 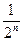PQ. По аксиоме Архимеда существует такие точки А_к и А_к+1, что _.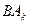

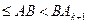· Аналогично на луче ВС отложим отрезки 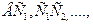равные отрезку РР_n: и рассмотрим точк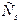и и 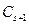такие, что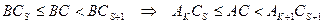

· Используя утверждение 1, имеем, что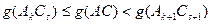

· Используя утверждение 2, имеем:

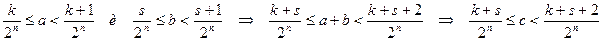
· Из последних соотношений имеем, что 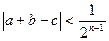. Пришли к противоречию, следовательно,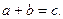

Лемма 15.4. Пусть установлено изменение отрезков с единицей измерения PQ. Если точки 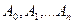расположены так, что 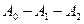, , 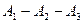… 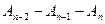и 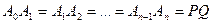, то длина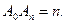

Лемма 15.5. Пусть установлено измерение отрезков. Если 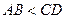, то .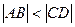

Лемма 15.6. Пусть установлено измерение отрезков. Если точка О – середина отрезка АВ, то .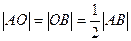

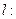
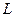
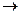
Теорема 15.7. (теорема единственности)если выбран единичный отрезок PQ, то существует не более одного отображения 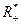, удовлетворяющего трем аксиомам измерения отрезков.

Доказательство. (Метод от противного)

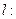
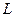
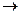
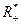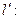
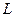
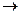
1. Допустим, что существуют два отображения и 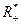, удовлетворяющие аксиомам 1-3. Отсюда, в частности, следует, что .

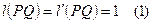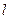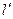2. Так как и различные отображения, то существует отрезок АВ, такой, что 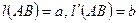и 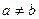. Допустим для определенности, что .

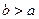3. На луче АВ отложим последовательно отрезки 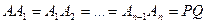, причем число 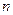выберем так, чтобы 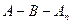, а точка 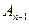принадлежала бы отрезку АВ. Тогда по аксиоме Архимеда такое число 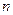существует. По лемме 15.4. и в силу равенств (1) имеем: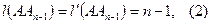 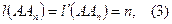. Из равенства (2) следует, что В и А_n-1 - различные точки, поэтому 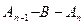, т.е. 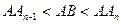. По лемме 15.5 имеем, что 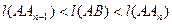. Учитывая равенства (2) и (3) .

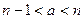4. Аналогично, для отображения 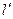получаем: 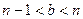. Таким образом,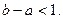

5. Пусть Р₁ – середина отрезка 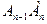. Тогда по аксиоме 2 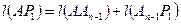. Учитывая равенство (2) и лемму 15.6, получаем 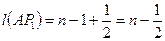. Аналогично, 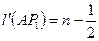. Следовательно, точка 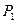не совпадает с точкой 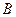, поэтому либо 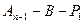, либо 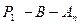. В первом случае 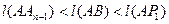, и по лемме 15.5 имеем 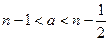. Аналогично 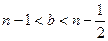. Таким образом, 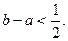Во втором случае приходим к такому же неравенству.

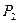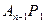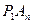6. Рассмотрим середину того из отрезков и , которому принадлежит точка 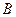. Рассуждая аналогично предыдущему, получим 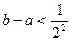. Продолжая рассуждения, через 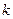шагов приходим к неравенству 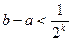, где 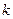- натуральное число. Получили противоречие. В самом деле, так как 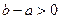, то всегда можно выбрать 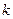настолько большим, чтобы 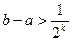. Предположение о том, что отображения 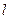и 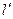различные, неверны.