Интегральная теорема Гаусса-Остроградского
Получение дифференциальных уравнений гидромеханики из законов сохранения, записанных в интегральной форме, основано на теореме Гаусса-Остроградского.
Пусть 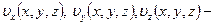 компоненты некоторого непрерывно дифференцируемого векторного поля
компоненты некоторого непрерывно дифференцируемого векторного поля 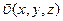 ;
; 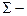 произвольная гладкая замкнутая поверхность, ограничивающая объем пространства V и имеющая, внешнюю нормаль
произвольная гладкая замкнутая поверхность, ограничивающая объем пространства V и имеющая, внешнюю нормаль 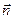 . Тогда имеет место равенство
. Тогда имеет место равенство
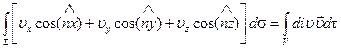 . (5.1)
. (5.1)
Иными словами, теорема Гаусса-Остроградского позволяет преобразовать интеграл по поверхности 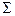 в интеграл по объему
в интеграл по объему 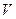 , ограниченному этой поверхностью.
, ограниченному этой поверхностью.
Поскольку интеграл
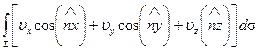
называют потоком вектора 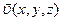 через поверхность
через поверхность 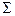 , а сумму трех частных производных
, а сумму трех частных производных
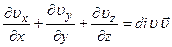 ,
,
вычисленных в точке 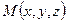 - дивергенцией вектора
- дивергенцией вектора 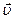 , то поток вектора
, то поток вектора 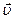 через замкнутую поверхность
через замкнутую поверхность 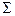 равен интегралу от дивергенции этого вектора по объему
равен интегралу от дивергенции этого вектора по объему 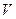 , заключенному внутри нее.
, заключенному внутри нее.
Для бесконечно малого объема 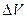 , заключающего в себе точку
, заключающего в себе точку 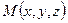 , справедлива формула
, справедлива формула
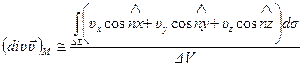
или
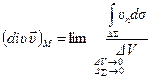 . (5.2)
. (5.2)
Если вектор 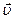 представляет скорость жидкости, то поток вектора через замкнутую поверхность
представляет скорость жидкости, то поток вектора через замкнутую поверхность 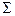 имеет смысл объема жидкости, вытекающей (если
имеет смысл объема жидкости, вытекающей (если 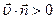 ) или втекающей (если
) или втекающей (если 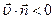 ) из объема
) из объема 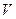 , ограниченного этой поверхностью, в единицу времени. Рассчитанный на единицу объема пространства он имеет смысл увеличения (если
, ограниченного этой поверхностью, в единицу времени. Рассчитанный на единицу объема пространства он имеет смысл увеличения (если 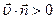 ) или уменьшения (если
) или уменьшения (если 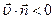 ) объема жидкости («дивергенция» буквально означает «расхождение») в каждой точке пространства. Таким образом, понятен смысл дивергенции вектора как скорости изменения объема жидкости в данной точке пространства. В частности, для несжимаемой жидкости, суммарный объем которой внутри замкнутой поверхности неизменен,
) объема жидкости («дивергенция» буквально означает «расхождение») в каждой точке пространства. Таким образом, понятен смысл дивергенции вектора как скорости изменения объема жидкости в данной точке пространства. В частности, для несжимаемой жидкости, суммарный объем которой внутри замкнутой поверхности неизменен, 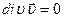 в каждой точке пространства, ограниченного этой поверхностью.
в каждой точке пространства, ограниченного этой поверхностью.
5.2. Дифференциальное уравнение неразрывности
Это уравнение выражает собой закон сохранения массы среды, и оно уже было получено в главе 1. Рассмотрим вывод это того уравнения, использующий интегральное представление.
В интегральной форме закон сохранения массы имеет вид (4.1)
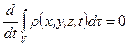
или
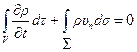 .
.
Используя формулу Гаусса-Остроградского, можно записать

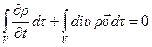 ,
,
или
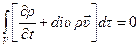
Поскольку объем 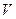 произволен, то должно выполняться равенство
произволен, то должно выполняться равенство
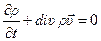 . (5.3)
. (5.3)
Это уравнение называется дифференциальным уравнением неразрывности (непрерывности) потока и представляет собой первое уравнение полной системы гидродинамических уравнений. В развернутом виде оно записывается так:
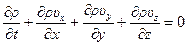 . (5.4)
. (5.4)
Таким образом, четыре функции координат и времени 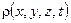 ,
, 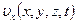 ,
, 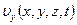 ),
), 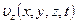 удовлетворяют этому уравнению с частными производными.
удовлетворяют этому уравнению с частными производными.
Для несжимаемой жидкости плотность у каждой частицы не изменяется. Поэтому полная производная по времени от 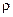 равна нулю
равна нулю
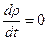 .
.
Преобразуя уравнение неразрывности (5.4), получаем:
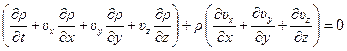 .
.
Первый член в левой части этого уравнения представляет собой полную производную по времени от плотности (см. 1.8)
равную нулю. Поэтому имеем
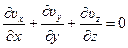 , (5.5)
, (5.5)
т.е. для несжимаемой жидкости дивергенция вектора скорости тождественно равна нулю: 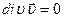 .
.
Дата добавления: 2016-05-16; просмотров: 1384;
