Течение идеальной жидкости.

Уравнения Эйлера

Наиболее просто замкнутая система дифференциальных уравнений записывается в случае модели идеальной жидкости (см. гл. 3), используемой в задачах гидромеханики, в которых касательные напряжения (например, напряжения трения) намного меньше, чем нормальные (силы давления), и поэтому могут не учитываться. Для получения модели идеальной жидкости следует положить

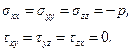
Тогда получается система четырех уравнений

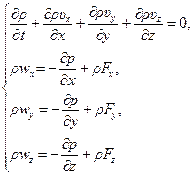(5.9)

для пяти неизвестных функци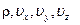й и .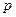

В общем случае для замыкания этой системы уравнений используется связь между плотностью жидкости и давлением. Если эта связь не содержит температуру

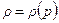(5.10)

(такая жидкость называется баротропной), то получается замкнутая система пяти уравнений (5.9) - (5.10) для определения пяти функций. В частности, для однородной несжимаемой жидкости, движущейся в условиях изотермического режима, система уравнений особенно упрощается и принимает вид:

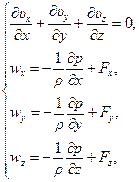(5.10)

где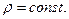

Существует большей раздел гидромеханики, посвященный решению различных задач в рамках модели идеальной жидкости. К числу таких задач относится большинство проблем газовой динамики, аэромеханики и др.

Если зависимость плотности от давления содержит температуру, то уравнений (5.9), (5.10) недостаточно для получения замкнутой системы уравнений, поскольку появляется еще одна неизвестная функция — температура. В этом случае необходимо привлекать к рассмотрению уравнение, выражающее закон сохранения энергии (4.49).