Формула В.Г.Шухова.
Применим полученное уравнение (4.57) для расчета распределение температуры 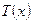 по длине участка трубопровода с постоянным диаметром
по длине участка трубопровода с постоянным диаметром 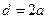 при установившемся неизотермическом течении несжимаемой жидкости. Выберем контрольную поверхность
при установившемся неизотермическом течении несжимаемой жидкости. Выберем контрольную поверхность 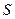 , состоящую из трех частей:
, состоящую из трех частей: 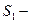 поперечное сечение трубы
поперечное сечение трубы 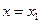 ;
; 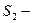 поперечное сечение трубы
поперечное сечение трубы 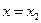 ;
; 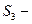 внутренняя поверхность трубы на участке
внутренняя поверхность трубы на участке 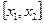 , причем
, причем 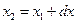 (рис. 4.14).
(рис. 4.14).

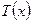
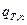
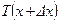
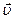
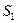
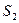
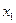
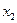
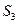
Рис. 4.14. Неизотермическое установившееся течение
жидкости в трубопроводе
Поскольку на 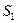 :
: 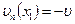 , на
, на 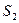 :
: 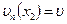 и на
и на 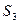 :
: 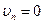 , то из (4.54) получаем:
, то из (4.54) получаем:
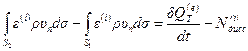 .
.
Далее имеем:
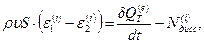
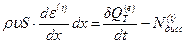 . (4.58)
. (4.58)
Примем следующие допущения:
а) Внутренняя энергия жидкости с точностью до постоянной величины определяется равенством
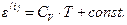 ,
,
где 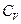 — теплоемкость жидкости при постоянном объеме (
— теплоемкость жидкости при постоянном объеме ( 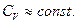 );
); 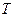 — абсолютная температура;
— абсолютная температура;
б) Приток внешнего тепла происходит только через поверхность трубы 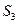 и определяется интегралом
и определяется интегралом
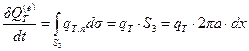 ,
,
где 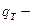 секундный поток тепла через единицу поверхности трубы, (
секундный поток тепла через единицу поверхности трубы, ( 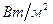 ).
).
в) Секундный поток тепла 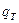 пропорционален разности температур
пропорционален разности температур 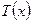 жидкости в трубе и окружающей среды
жидкости в трубе и окружающей среды 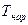 (формула Ньютона), так что
(формула Ньютона), так что
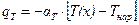 . (4.59)
. (4.59)
Коэффициент 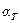 , входящий в формулу (4.59), называется коэффициентом теплопередачи. Знак минус показывает, что тепло передаются в направлении от большей температуры к меньшей:
, входящий в формулу (4.59), называется коэффициентом теплопередачи. Знак минус показывает, что тепло передаются в направлении от большей температуры к меньшей: 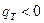 , если
, если 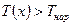 (отбор тепла от жидкости в трубе);
(отбор тепла от жидкости в трубе); 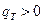 , если
, если 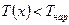 (приток тепла к жидкости в трубе);
(приток тепла к жидкости в трубе);
г) Суммарная мощность 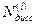 диссипативных сил вязкого внутреннего трения между сечениями
диссипативных сил вязкого внутреннего трения между сечениями 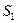 и
и 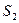 можно представить как произведение
можно представить как произведение 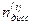 мощности этих сил в единице массы жидкости (удельной мощности) и массы жидкости
мощности этих сил в единице массы жидкости (удельной мощности) и массы жидкости 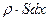 :
:
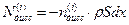 .
.
Используя принятые допущения, получаем из уравнения (4.58) уравнение
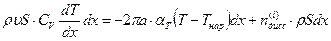 ,
,
которое после деления на 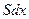 дает дифференциальное уравнение для температуры
дает дифференциальное уравнение для температуры 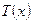 :
:
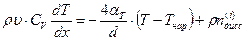 . (4.60)
. (4.60)
Уравнение (4.60) может быть проинтегрировано в случае, если принять, что 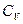 ,
, 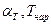 и
и 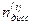 есть постоянные величины. Кроме того,
есть постоянные величины. Кроме того, 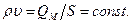
Если в начальном сечении трубопровода 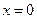 температура жидкости равна
температура жидкости равна 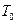 , то решение этого уравнения имеет вид:
, то решение этого уравнения имеет вид:
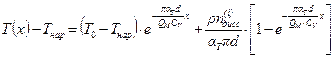 , (4.61)
, (4.61)
где 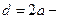 внутренний диаметр трубопровода.
внутренний диаметр трубопровода.
Формула (4.61) носит название формула В. Г. Шухова. (В.Г.Шухов - выдающийся русский инженер, архитектор, изобретатель и ученый, 1853-1939). Первое слагаемое в правой части этой формулы определяет изменение температуры жидкости за счет теплообмена с окружающей средой, второе слагаемое связано с нагреванием жидкости за счет диссипации механической энергии.
Вводя параметр 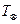 :
:
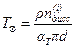 ,
,
имеющий размерность температуры и отражающий переход механической энергии в тепло, формулу В.Г.Шухова можно записать проще:
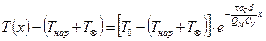 . (4.62)
. (4.62)
Эта формула показывает, что выделение тепла при трении слоев жидкости друг относительно друга эквивалентно увеличению наружной температуры на величину 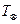 .
.
Распределение температуры 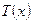 по длине участка трубопровода показано на рис. 4.16 [ ]. Из графиков на этом рисунке видно, что в случае
по длине участка трубопровода показано на рис. 4.16 [ ]. Из графиков на этом рисунке видно, что в случае 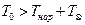 жидкость, текущая в трубопроводе, охлаждается, наоборот, в случае, когда
жидкость, текущая в трубопроводе, охлаждается, наоборот, в случае, когда 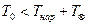 , жидкость нагревается. В обоих случаях
, жидкость нагревается. В обоих случаях 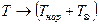 .
.
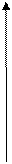 Т
Т


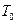

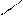
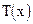
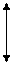



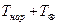
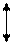


 T0
T0 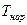
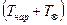

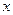
Рис.4.16. Распределение температуры
по длине участка трубопровода
Температуру 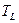 жидкости в конце участка трубопровода можно вычислить с помощью решения (4.62), положив в нем
жидкости в конце участка трубопровода можно вычислить с помощью решения (4.62), положив в нем 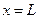 . Имеем:
. Имеем:
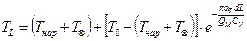 , (4.63)
, (4.63)
где 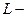 длина участка.
длина участка.
4.6. Закон изменения момента количества движения
Движение любой механической системы удовлетворяет еще одному общему закону механики – закону об изменении момента количества движения. Этот закон читается так: производная по времени от главного вектора момента количества движения системы материальных точек равна сумме моментов всех внешних сил, приложенных к этой системе. В случае течения жидкости внутри вращающихся сосудов использование этого закона пзволяет получать весьма полезные результаты.
Применим теорему об изменении момента количества движения системы материальных точек к индивидуальному объему жидкости. Полагая в формуле (4.6) 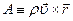 , запишем эту теорему в следующем виде:
, запишем эту теорему в следующем виде:
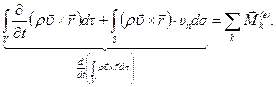 (4.64)
(4.64)
Если течение жидкости установившееся, то 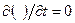 , поэтому из уравнения (4.40) исчезает первое слагаемое в левой части, а само уравнение можно трактовать как уравнение баланса моментов количества движения в объеме жидкости, ограниченном контрольной поверхностью
, поэтому из уравнения (4.40) исчезает первое слагаемое в левой части, а само уравнение можно трактовать как уравнение баланса моментов количества движения в объеме жидкости, ограниченном контрольной поверхностью 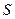 :
:
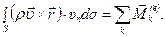 (4.65)
(4.65)
Уравнение Л.Эйлера для насоса
Применим закон об изменении момента количества движения к установившемуся течению жидкости через рабочее колесо центробежного насоса.
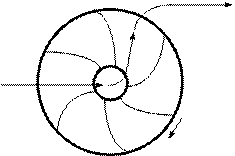
Центробежные насосы явлются частным случаем устройств, создающих напор. Как и всякое такое устройство, центробежный насос заставляет жидкость двигаться в направлении против напора, затрачивая для этого определенное количество энергии. Центробежный насос забирает жидкость в сечении всасывания, где давление в жидкости низкое, и заставляет ее перемещаться к сечению нагнетания, где давление в жидкости высокое. Конечно, сама по себе жидкость не будет перемещаться против давления, для этого требуется принуждающая сила. В случае центробежного насоса такой принуждающей силой являяется центробежная сила инерции, действующая на жидкость внутри быстро вращающегося рабочего колеса (ротора) насоса (рис. 4.17).
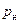
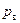 1
1
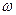
Рис. 4.17. Принцип действия центробежного насоса
Жидкость с низким давлением 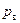 поступает в полость 1 рабочего колеса вблизи его центра, движется под действием центробежной силы инерции вдоль профилированных лопаток колеса от центра к периферии 2 в направлении против давления и выходит из колеса в трубопровод с повышенным давлением
поступает в полость 1 рабочего колеса вблизи его центра, движется под действием центробежной силы инерции вдоль профилированных лопаток колеса от центра к периферии 2 в направлении против давления и выходит из колеса в трубопровод с повышенным давлением 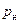 .
.
Если предположить, что угловая скорость 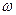 вращения рабочего колеса насоса есть постоянная величина, а течениежидкости – струйное, в котором линии тока повторяют очертание лопаток колеса, то скорости течения и давления являются функциями только радиальной координаты и не зависят от времени, следовательно, течение жидкости внутри рабочего колеса можно считать установившимся. Будем считать также, что турбулизация течения и гидравлические потери отсутствуют.
вращения рабочего колеса насоса есть постоянная величина, а течениежидкости – струйное, в котором линии тока повторяют очертание лопаток колеса, то скорости течения и давления являются функциями только радиальной координаты и не зависят от времени, следовательно, течение жидкости внутри рабочего колеса можно считать установившимся. Будем считать также, что турбулизация течения и гидравлические потери отсутствуют.
Выберем контрольную поверхность 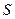 состоящей из двух частей, двух соосных цилиндров
состоящей из двух частей, двух соосных цилиндров 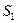 и
и 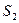 (рис. 4.18), через первую поверхность жидкость входит в колесо центробежного насоса, через вторую - выходит из колеса. Жидкость, движущаяся в рабочем колесе насоса, участвует в двух движениях: вместе с колесом (переносное движение) и относительно колеса (относительное движение). Абсолютная скорость
(рис. 4.18), через первую поверхность жидкость входит в колесо центробежного насоса, через вторую - выходит из колеса. Жидкость, движущаяся в рабочем колесе насоса, участвует в двух движениях: вместе с колесом (переносное движение) и относительно колеса (относительное движение). Абсолютная скорость 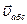 частиц жидкости равна сумме двух скоростей – скорости переносного движения
частиц жидкости равна сумме двух скоростей – скорости переносного движения 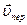 , т.е. скорости той точки колеса, с которой частица совпадает в данный момент, и скорости
, т.е. скорости той точки колеса, с которой частица совпадает в данный момент, и скорости 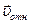 относительного движения жидкости вдоль лопаток колеса, так что
относительного движения жидкости вдоль лопаток колеса, так что 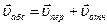 .
.
Обозначим: 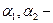 острые углы между вектором абсолютной скорости
острые углы между вектором абсолютной скорости 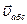 и касательными к окружностям
и касательными к окружностям 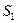 и
и 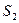 , соответственно;
, соответственно; 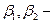 острые углы между вектором относительной скорости
острые углы между вектором относительной скорости 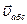 и касательными к окружностям
и касательными к окружностям 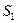 и
и 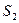 , соответственно, рис. 4.18. Углы
, соответственно, рис. 4.18. Углы 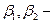 это углы наклона лопаток колеса к окружностям
это углы наклона лопаток колеса к окружностям 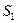 и
и 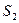 , соответственно, т.е. они определяются конструкцией рабочего колеса насоса.
, соответственно, т.е. они определяются конструкцией рабочего колеса насоса.

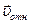
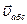
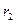
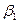
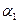
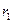
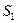
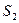
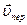
Рис. 4.18. План скоростей в рабочем колесе насоса
Применим уравнение (4.65) к контрольному объему жидкости в колесе. Вычислим левую часть этого уравнения, в которой стоит разность 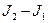 моментов количества движения вытекающего и втекающего в контрольный объем. Поскольку течение происходит в плоскости чертежа, то все моменты (как скоростей, так и сил) направлены по оси, перепендикулярной плоскости чертежа. Имеем:
моментов количества движения вытекающего и втекающего в контрольный объем. Поскольку течение происходит в плоскости чертежа, то все моменты (как скоростей, так и сил) направлены по оси, перепендикулярной плоскости чертежа. Имеем:
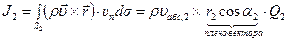 ,
,
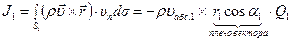 ,
,
следовательно,
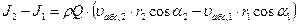 . (4.66)
. (4.66)
Здесь учтено, что 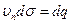 и
и 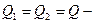 объемный расход жидкости (подача насоса).
объемный расход жидкости (подача насоса).
На массу жидкости, заполняющей межлопастные каналы рабочего колеса, действуют внешние силы: силы тяжести, силы давления на контрольных поверхностях 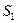 ,
, 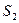 , силы реакции поверхностей лопаток рабочего колеса, а также силы трения жидкости на обтекаемых поверхностях. Момент сил тяжести всегда равен нулю, т.к. плечо этих сил равно нулю (они проходят через ось вращения колеса). Момент сил давления в расчетных сечениях по этой же причине также равен нулю. Следовательно, момент всех внешних сил относительно оси вращения колеса сводится к моменту
, силы реакции поверхностей лопаток рабочего колеса, а также силы трения жидкости на обтекаемых поверхностях. Момент сил тяжести всегда равен нулю, т.к. плечо этих сил равно нулю (они проходят через ось вращения колеса). Момент сил давления в расчетных сечениях по этой же причине также равен нулю. Следовательно, момент всех внешних сил относительно оси вращения колеса сводится к моменту 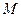 динамического воздействия рабочего колеса на протекающую через него жидкость
динамического воздействия рабочего колеса на протекающую через него жидкость
Уравнение (4.65) приобретает вид:
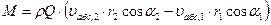 , (4.67)
, (4.67)
где 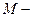 проекция вектора момента всех внешних сил, действующих на колесо, на ось, перепендикулярную плоскости чертежа.
проекция вектора момента всех внешних сил, действующих на колесо, на ось, перепендикулярную плоскости чертежа.
Если обе части этого уравнения умножить на угловую скорость 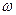 вращения колеса, то произведение
вращения колеса, то произведение 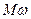 даст мощность
даст мощность 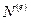 , передаваемую жидкости насосом, названную в п. 4.4 мощностью сторонних сил:
, передаваемую жидкости насосом, названную в п. 4.4 мощностью сторонних сил: 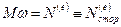 .
.
Если потери в насосе отсутствуют, то из уравнения Бернулли следует равенство
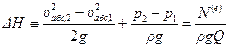 , (4.68)
, (4.68)
поэтому уравнение (4.67) можно записать в виде:
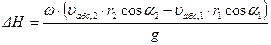 .
.
Учитавая, что 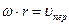 , приходим к уравнению
, приходим к уравнению
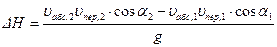 , (4.69)
, (4.69)
называемому уравнением Л.Эйлера. Это уравнение является одним из основных уравнений в теории насов.
Если известны конструктивные параметры насоса 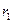 и
и 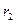 ,
, 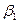 и
и 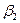 ,
, 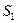 и
и 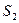 , а также его подача
, а также его подача 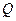 и угловая скорость
и угловая скорость 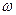 вращения рабочего колеса, то все гидравлические параметры, входящие в уравнение (4.69), рассчитываются по следующим формулам:
вращения рабочего колеса, то все гидравлические параметры, входящие в уравнение (4.69), рассчитываются по следующим формулам:
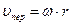 ,
, 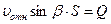 ,
, 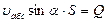 ,
,
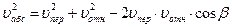 .
.
Уравнение Л.Эйлера можно записать также в терминах давлений. С учетом (4.68) имеем:
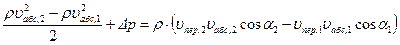 ,
,
откуда следует выражение для разности 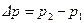 давлений на периферии и в центре рабочего колеса насоса:
давлений на периферии и в центре рабочего колеса насоса:
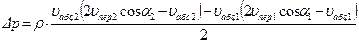 . (4.70)
. (4.70)
Если, 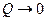 , то
, то 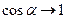 ,
, 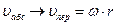 , поэтому максимально возможное значение
, поэтому максимально возможное значение 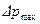 перепада давлений, которое может иметь данный насос, дается выражением:
перепада давлений, которое может иметь данный насос, дается выражением:
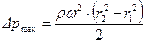 . (4.71)
. (4.71)
Заметим, что в действительности напор и давление, развиваемые насосом, меньше теоретических значений, т.к. реальные условия работы насоса отличаются от идеальных, принятых при выводе уравнения (прежде всего, наличием гидравлических потерь). Обычно это обстоятельство учитывается введением в формулы (4.69) и (4.70) поправочных коэффициентов.
Пример. Какое максимальное дифференциальное давление может развить нефтяной насос НМ 5000-210, рассчитанный на перекачку 5000 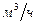 нефти (
нефти ( 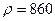
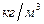 ), если известно, что внешний и внутренний диаметры его рабочего колеса
), если известно, что внешний и внутренний диаметры его рабочего колеса
равны 440 и 100 мм, соответственно, а число 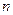 оборотов в минуту составляет 2950?
оборотов в минуту составляет 2950?
Решение. Находим угловую скорость 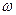 вращения рабочего колеса насоса:
вращения рабочего колеса насоса:
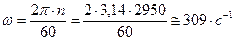 .
.
По формуле (4.71) вычисляем 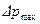 :
:
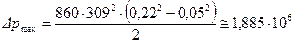 (Па),
(Па),
что составляет 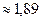 МПа или 19,21 атм. Если перевести это давление в дифференциальный напор насоса, то он окажется равным
МПа или 19,21 атм. Если перевести это давление в дифференциальный напор насоса, то он окажется равным 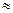 223 м.
223 м.
Ответ: 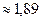 МПа.
МПа.
5. УРАВНЕНИЯ ГИДРОМЕХАНИКИ В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ
В предыдущих разделах рассматривалось применение общих теорем механики системы материальных точек к подвижному объему жидкости, то есть объему сплошной среды, состоящему из одних и тех же частиц. Основные законы механики — закон сохранения массы, закон изменения количества движения, закон изменения энергии, сформулированные в виде соотношений (4.1-4.3) и (4.43), называют уравнениями динамики среды в интегральной форме.
Важно иметь в виду, что подвижный объем 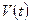 , фигурирующий в этих формулах, произвольный. Если использовать это обстоятельство, то из соотношений (4.1-4.3) и (4.49) можно получить намного больше информации, чем это было сделано до сих пор, при рассмотрении некоторых задач гидравлики. В основе получения такой информации лежит известная из курса математического анализа теорема о том, что если интеграл от непрерывной функции
, фигурирующий в этих формулах, произвольный. Если использовать это обстоятельство, то из соотношений (4.1-4.3) и (4.49) можно получить намного больше информации, чем это было сделано до сих пор, при рассмотрении некоторых задач гидравлики. В основе получения такой информации лежит известная из курса математического анализа теорема о том, что если интеграл от непрерывной функции 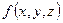 , вычисленный по любой произвольной области
, вычисленный по любой произвольной области 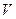 , равен нулю, то в этой области тождественно равна нулю подынтегральная функция
, равен нулю, то в этой области тождественно равна нулю подынтегральная функция 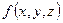 , то есть из равенства
, то есть из равенства
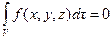
( 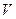 — произвольный объем) следует равенство
— произвольный объем) следует равенство
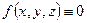 .
.
Таким образом, если между гидродинамическими параметрами сплошной среды существуют интегральные соотношения, справедливые для любого объема 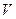 , то в каждой точке пространства, занятого этой средой, должны существовать соотношения между локальными значениями этих параметров, т.е. значениями, вычисленными в этой точке. Такие соотношения, как будет показано ниже, дают систему дифференциальных уравнений механики сплошной среды. Примером могут служить дифференциальные уравнения движения сплошной среды в напряжениях (1.30), полученные в гл. 1.
, то в каждой точке пространства, занятого этой средой, должны существовать соотношения между локальными значениями этих параметров, т.е. значениями, вычисленными в этой точке. Такие соотношения, как будет показано ниже, дают систему дифференциальных уравнений механики сплошной среды. Примером могут служить дифференциальные уравнения движения сплошной среды в напряжениях (1.30), полученные в гл. 1.
Дата добавления: 2016-05-16; просмотров: 8652;
