Закон изменения полной энергии

Теорема живых сил, речь о которой шла в предыдущем параграфе, представляет собой закон изменения кинетической энергии системы материальных точек, являющийся следствием законов механики. Однако существует другой, более фундаментальный закон физики – закон об изменении полной энергии тела, составляющий так называемое первое начало термодинамики. Этот закон гласит: изменение полной энергии любого тела (твердого, жидкого, газообразного и т.д.) равно сумме работы внешних сил и внешнему притоку тепла. Иными словами, закон об изменении полной энергии тела утверждает, что изменить эту энергию можно только за счет притока (или оттока) энергии извне - либо в виде работы внешних сил, либо в виде внешнего тепла, либо того и другого вместе взятых. В случае если работа внешних сил и приток внешнего тепла отсутствуют, полная энергия тела не изменяется. Последнее утверждение известно как закон сохранения полной энергии тела.

Относя притоки энергии к единице времени, можно говорить об интенсивности 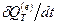притока внешнего тепла и о мощности 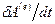внешних сил:

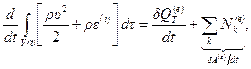(4.53)

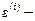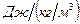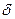где плотность внутренней энергии - внутренняя энергия единицы массы среды, ; интенсивность притока внешнего тепла (Вт). Символ используется здесь, чтобы подчеркнуть, что в общем случае величины 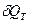и 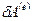не являются полными дифференциалами каких-либо функций; функций состояния 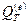и 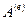не существует.

Уравнение (4.53), представляющее выражение 1-го начала термодинамики, читается так: скорость изменения полной энергии системы материальных частиц, составляющих подвижный объем 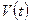, равна интенсивности притока внешнего тепла, сложенной с суммарной мощностью всех внешних сил. Важно подчеркнуть, что в этот закон входят только внешниепритоки энергии.

Если из уравнения (4.53) исключить изменение кинетической энергии с помощью уравнения (4.3), то получится уравнение, называемое уравнением притока тепла:

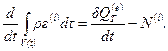(4.54)

В это уравнение, определяющее скорость изменения внутренней энергии объема жидкости V(t), входят интенсивность внешнего притока тепла и мощность внутренних сил.

Преобразуя левую часть уравнения (4.54) с помощью основной формулы (4.10), получаем:

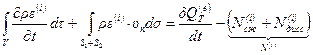. (4.55)

Для несжимаемой жидкости 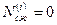, поэтому уравнение (4.55) имеет вид:

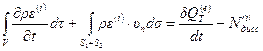. (4.56)

Если рассматривать к тому же установившееся течение жидкости, для которого , то уравнение упрощается еще больше:

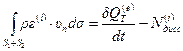. (4.57)