Диссипативные системы. Основные определения и теоремы.

Пусть дана нелинейная нестационарная система, в общем случае не допускающая тривиального решения и имеющая вид

(*)

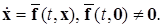В частности, система (*) может допускать представление в виде так называемой «системы с возмущением»

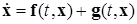(2.4.1)

с областью определения правых частей системы вида

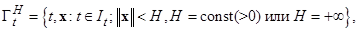(2.4.2)

в которой вектор-функция 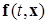представляет правые части системы «без возмущения», а вектор-функция 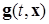- «возмущение», причем:

1. вектор-функция 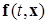системы «без возмущения» удовлетворяет в области (2.4.2) всем условиям существования и единственности решений, проходящих через любую точку 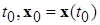из области 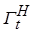, и допускает тривиальное решение, т.е.:

а) f- непрерывна по t и x;

б) f- непрерывно дифференцируема по xи

(вследствие непрерывности по известной теореме

Вейерштрасса)

все частные производные ,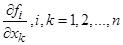

ограничены на любом компактном подмножестве (2.4.3)

из области (2.4.2);

в) 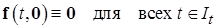, т.е. система без возмущения и

допускает тривиальное решение .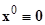

2. вектор-функция 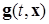- неизвестное «возмущение», удовлетворяющее лишь требованию быть «ограниченной по норме», в области (2.4.2), т.е.:

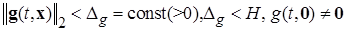. (2.4.4)

Сначала дадим определение диссипативности для системы общего вида (*), не допускающей тривиального решения, и сформулируем теорему о достаточных условиях диссипативности для такой систем, опубликованную Т. Йосидзавой в 1955 г., а затем сформулируем теорему, дающую конструктивные условия достаточности диссипативности системы, допускающей приведенное выше представление нелинейной нестационарной системы общего вида (*) в виде нелинейной нестационарной системы с «возмущением» (2.4.1)-(2.4.4.).

Определение диссипативной системы. Система (*) вида 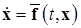называется диссипативной системой, если существует некоторое положительное число 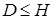(D-окрестность 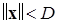), такое, что все решения 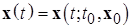, удовлетворяющие неравенству:

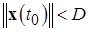, (2.4.5)

т. е. все решения 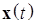, начинающиеся внутри D-окрестности (внутри сферы 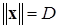), удовлетворяют следующим условиям:

(1) они бесконечно продолжимы вправо;

(2) существует положительное число d (d-окрестность 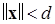), , 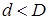такое, что каждое решение 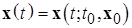, удовлетворяющее неравенству (2.4.5), удовлетворяет при 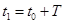и неравенству вида

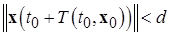, (2.4.6)

где 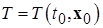– некоторый интервал времени, выбор которого зависит от выбора 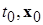, т. е. для каждого решения 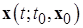существует момент времени 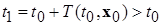, после которого оно навсегда погружается в d-окрестность . ■

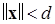Замечание. Отметим, что речь идет не о диссипативности некоторого фиксированного решения 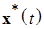системы (*), а о свойстве диссипативности всех решений системы (*), т. е. речь идет о существовании для системы (*) двух фиксированных сфер 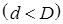таких, что все решения, начинающиеся из D-сферы 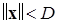со временем «навечно» погружаются в d-сферу 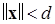, и условие (2.4.6) можно записать в виде эквивалентного соотношения для верхнего предела:

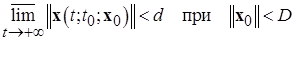. (2.4.7)

D-сфера называется областью диссипативности, а d-сфера называется предельным множеством диссипативной системы (*)

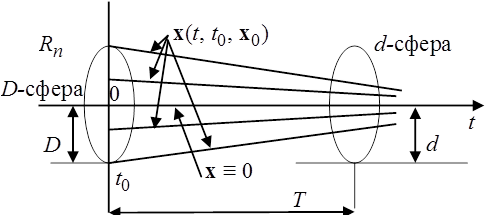
Рисунок 7

Замечание. Решения диссипативной системы иногда называют предельно (финально) ограниченными. ■

Теорема о достаточных условиях диссипативности нелинейной нестационарной системы общего вида (Т. Йосидзава, 1955)

Пусть дана система (*), правая часть которой 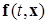суть вещественная вектор-функция, удовлетворяющая условиям непрерывности по 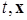и непрерывной дифференцируемости по 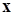в области (2.4.2), обеспечивающим существование и единственность решений 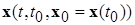, проходящих через любую точку .

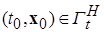Пусть также в области (2.4.2) задан некоторый полубесконечный цилиндр-трубка 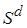радиуса 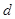, окружающая ось времени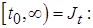

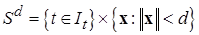(2.4.8)

где знак «×» - знак декартова умножения множеств, и пусть во внешности цилиндра (2.4.8) для системы (*) существует (найдена) функция Ляпунова 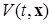и три функции Хана 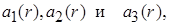такие, что выполняются следующие условия всюду в 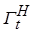вне цилиндра (2.4.8):

1) 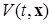- непрерывно дифференцируема по 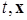в области ;

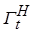2) 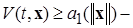положительная определенность и ББНП при ;

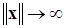3) 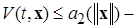сильный БМВП при ;

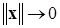4) 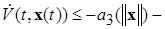отрицательная определенность полной производной по времени t функции 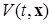, вычисленной в силу системы (*).

Тогда нелинейная нестационарная система (*) диссипативна в смысле данного выше определения равномерно относительно начального момента времени 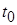, т.е. число 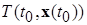из определения диссипативной системы можно выбрать зависящие только от 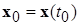, с областью диссипативности 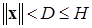и предельным множеством .■

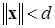(Доказательство см. [2, с.с. 294-297]).

Теорема Т. Йосидзавы не дает практически полезных оценок времени сходимости решений диссипативной системы в полубесконечный цилиндр-трубку (2.4.8) радиуса 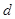, окружающую ось времени – предельное множество 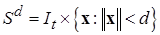диссипативной системы, но зато пролагает путь к получению более конструктивных условий диссипативности, а именно, имеет место следующее определение.

Определение экспоненциально диссипативной системы. Система (*), диссипативная в смысле данного выше определения, называется экспоненциально диссипативной системой, если все решения 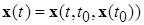, начинающиеся в области диссипативности, т.е. удовлетворяющие неравенству

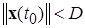, (2.4.9)

всюду вне цилиндра-трубки (2.4.8) подчиняются соотношению

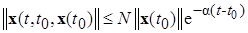(2.4.10)

где 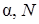- некоторые положительные числа, выбор которых не зависит от выбора решений 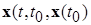, т.е. существуют такие 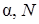, что все решения, исходящие из сферы 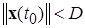, удовлетворяют неравенству – экспоненциальной оценке вида (2.4.10) до тех пор, пока они не попадут внутрь полубесконечного цилиндра-трубки (2.4.8).■

Опираясь на данное определение, сформулируем теорему, дающую практически полезный критерий экспоненциальной диссипативности для частного случая системы (*) – нелинейной нестационарной системы «с возмущением» вида (2.4.1)÷(2.4.4).