Вопрос 3. Канторович Л.В.: разработка теории линейного программирования

Леонид Витальевич Канторович (1912-1986) родился в Санкт-Петербурге в семье врача. Его выдающиеся способности проявились рано — в 14 лет он поступил в Ленинградский государственный университет. Закончив ЛГУ за 4 года, он поступил в аспирантуру. В 1932 г. он становится доцентом, а в 1935 г. — профессором ЛГУ. В 1935 г. ему присвоено звание доктора физико-математических наук без защиты диссертации. В 1958 г. он избран членом-корреспондентом АН СССР по экономике, а в 1964 г. — академиком.

Серьезные занятия экономикой начались для Л.В. Канторовича с того, что в 1938 г. к нему за консультацией обратились несколько инженеров из лаборатории фанерного треста. Смысл их проблемы заключался в том, что при обработке различного сырья на разных лущильных станках получалась различная производительность и стояла задача максимизации выпуска продукции при заданном соотношении между ее видами. В современной терминологии эту проблему можно сформулировать как задачу максимизации линейной функции при наличии линейных ограничений. В простом случае решение легко найти перебором экстремальных точек допустимого множества, однако даже в задаче фанерного треста, при пяти станках и восьми видах сырья, это потребовало бы решения около миллиарда систем линейных уравнений.

Для решения предложенной ему задачи Л.В. Канторович в январе 1939 г. разработал специальный метод, при котором с каждым ограничением исходной задачи связывалась специальная оценка, называемая разрешающим множителем. Оптимальный план задачи определялся в результате итеративного процесса, в ходе которого происходила последовательная корректировка разрешающих множителей. Таким образом, Канторович открыл новый раздел математики — линейное программирование, изучающий задачи нахождения экстремума линейной функции на допустимом множестве, задаваемом линейными ограничениями и неравенствами, и предложил алгоритм решения таких задач.

Результаты своих исследований Канторович изложил в брошюре «Математические методы организации и планирования производства», опубликованной в 1939 г. В ней, наряду с задачей фанерного треста, получившей впоследствии наименование станковой, рассматривались и другие проблемы: наиболее полное использование механизмов, максимальное уменьшение отходов, наиболее рациональное использование топлива, наилучшее выполнение плана строительства, наилучшее распределение посевной площади, наилучший план перевозок. Метод Канторовича был пригоден для решения всех этих задач.

Идеи Л.В. Канторовича долго не признавались экономистами. Тем не менее Леонид Витальевич описал ряд важных с точки зрения экономической науки свойств этих множителей. Если продукт не дефицитен, соответствующий множитель равен нулю. Таким образом, множители выступают показателями дефицитности продукции. Они также являлись показателями эквивалентности для различных деталей, и с помощью множителей можно было определять, как влияют величины запасов сырья или выпуска деталей, выступающие в задаче в качестве ограничений, на оптимальное значение целевой функции.

До этого экономическая наука знала два вида эквивалентности разнородных потребительных стоимостей — по стоимости и по полезности. Разрешающие множители давали третий вид эквивалентности — по влиянию на целевую функцию, и вполне естественно, что впоследствии остро встал вопрос о его соотношении с первыми двумя.

В своей работе Л.В. Канторович рассмотрел возражения против применения математики в технико-экономических расчетах. Эти возражения были связаны с тем, что многие обстоятельства учесть математически невозможно, для применения метода разрешающих множителей нужно иметь много данных, они неточны, эффект от расчетов составляет всего 4-5%, применение метода порой невозможно из-за организационных препятствий. Л.В. Канторович же полагал, что с помощью его метода многое нужно учесть, что требуемые данные нужны и для нормальной плановой работы, поэтому их неточность не имеет большого значения. При массовом применении эффект от их использования был бы очень велик, даже если бы он составлял 1%.

По мнению Л.В. Канторовича, если будет доказана эффективность применения оптимального плана, то необходимые организационные изменения будут сделаны.

В 1940 г. он опубликовал математический вариант некоторых своих результатов. Из частных задач прежде всего следует выделить транспортную задачу. Работа, содержавшая ее решения, была подготовлена Л.В. Канторовичем и М.К. Гавуриным в 1940 г., однако из-за негативного отношения экономистов к математике в этот период ее долгое время не удавалось опубликовать. Абстрактный вариант транспортной задачи был опубликован Канторовичем в 1942 г. За разработку метода линейного программирования он был удостоен Нобелевской премии по экономике в 1975г.За разработку метода линейного программирования Леонид Витальевич Канторович (1912–1986) был (совместно с американским экономистом Т. Купмансом) удостоен Нобелевской премии в области экономики (1975 г.).

Заслуга Канторовича состоит в том, что он предложил математический метод поиска оптимального варианта распределения ресурсов. Решая конкретную задачу достижения наибольшей производительности при загрузке оборудования предприятия, производящего фанеру, ученый разработал метод, получивший название метода линейного программирования. Тем самым был открыт новый раздел в математике, получивший распространение в экономической практике, способствовавший развитию и использованию электронно-вычислительной техники.

Для решения задачи на оптимум Канторович использовал метод последовательных приближений, последовательного составления вариантов с выбором наилучшего в соответствии с условиями задачи. Линейное программирование – это программное распределение ограниченных ресурсов наилучшим способом в соответствии с поставленными целями.

Как найти этот наилучший способ? Как получить оптимальный результат и убедиться, что он действительно оптимален?

Предлагается построить математическую модель в виде формул, графика, таблицы. Затем подставить в модель конкретные числовые показатели и произвести вычисления. Многие взаимосвязи и процессы довольно схожи, однотипны. Это позволяет построить типовые модели, например модель транспортной задачи или распределительной задачи. При решении типовой задачи требуется найти такие значения нескольких вариантов, которые отвечают определенным условиям (ограничениям) и соответствующей цели.

Например, требуется с наименьшими затратами перевезти грузы от трех поставщиков к пяти потребителям. Задачу можно попытаться решить методом перебора многочисленных вариантов. Это потребует громоздких расчетов и немалого времени. Но мы не будем уверены, что избранный вариант оптимален.

Метод линейного программирования позволяет найти оптимальное решение. Линейным оно называется потому, что основывается на решении линейных уравнений. Неизвестные в них только первой степени; ни одно неизвестное не перемножается на другое неизвестное. Такие уравнения отражают зависимости, которые могут быть изображены на графике прямыми линиями.

На рис. 5 приведена транспортная задача: требуется определить план перевозок при минимальных затратах.

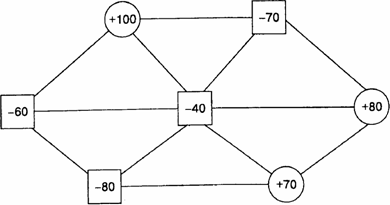
Рис. 5 Транспортная задача 151

В данном случае имеются четыре потребителя (квадратики) и три поставщика (кружочки). Линии, соединяющие пункты, изображают маршруты поставок (транспортную сеть). Цифры внутри квадратиков показывают объемы спроса (со знаком минус), внутри кружочков – размеры предложения (со знаком плюс).

Несколько иной целевой критерий в задаче о диете (кормовом рационе). Задача сводится к поиску оптимального рациона для кормления скотины или птицы. При постоянном изменении рыночных цен на корма фермеры подбирают оптимальный рацион при минимуме затрат, производя соответствующие расчеты на компьютере.

Для любой задачи линейного программирования существует сопряженная ей, двойственная задача. Если прямая задача заключается в минимизации целевой функции, то двойственная – в максимизации.

При непосредственном участии Канторовича и его ближайших коллег – В. В. Новожилова (автора идеи продуктово -трудового баланса) и В. С. Немчинова (обосновавшего глобальный критерий функционирования экономики) – формировалась отечественная экономико-математическая школа.

Усилиями экономистов-математиков была разработана система оптимального функционирования экономики (СОФЭ); строились модели эффективного распределения и оценки ресурсов.