Ранг, дефект линейного оператора.

Образ нуля равен нулю. Действительно, 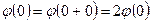, отсюда .

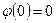Множество векторов из W, образ которых равен 0, называется ядром линейного оператора. Ядро линейного преобразования обозначим 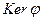( 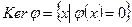). Ядро является подпространством W (докажите) и его размерность называют дефектом и обозначают .

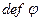Множество всех образов векторов из W обозначают 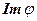( 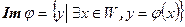). Множество образов является подпространством V (докажите), его размерность называют рангом линейного оператора и обозначают .

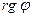Теорема 6.4. .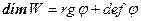

Доказательство. Пусть 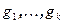– базис 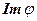. По определению 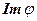для каждого вектора 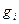существует прообраз 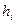из W. Система векторов 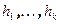является линейно независимой. Действительно, из равенства 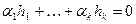, выводим 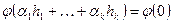, или

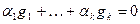. В силу линейной независимости, все коэффициенты равны 0, и система 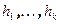является линейно независимой. Аналогично показывается, что пересечение линейной оболочки векторов 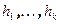и 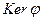состоит только из нулевого вектора. Действительно, из включения 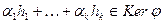, выводим 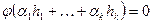, и далее, 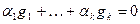. Для любого вектора x из W найдутся коэффициенты, что 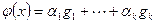, и 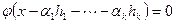. Таким образом W представляется в виде прямой суммы линейной оболочки векторов 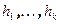и 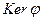. Теорема вытекает из свойства прямой суммы.

Следствие 6.1. Можно выбрать базисы в пространствах W и V так, чтобы матрица линейного оператора имела диагональный вид, причем по диагонали расположены 1 и 0. Количество ненулевых элементов на диагонали равно рангу оператора.

Доказательство. Пусть 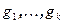и 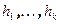имеют тот же смысл, что и в доказательстве предыдущей теоремы. Дополним векторы 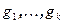до базиса V, а векторы 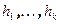до базиса W векторами из 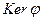. Полученные базисы обозначим через 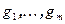и 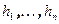, соответственно. Построим матрицу линейного оператора в этих базисах. Заметим, 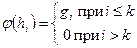, а координаты вектора 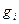в базисе 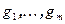равны (0,…,0,1,0,…,0), где 1 стоит на i-ом месте. Таким образом, матрица линейного оператора в этих базисах имеет диагональный вид, причем по диагонали расположены 1 и 0. Количество 1 равно рангу оператора.