Собственные векторы и собственные числа. Характеристическое уравнение.

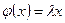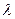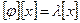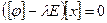Базис одномерного инвариантного подпространства называется собственным вектором. Другими словами, ненулевой вектор x называется собственным, если . Число называется собственным. Запишем это равенство в координатах , или . Последнее равенство можно рассматривать как квадратную систему линейных уравнений с n неизвестными. По правилу Крамера, если 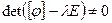, то система имеет единственное нулевое решение. Следовательно, собственные числа являются корнями уравнения 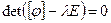. Данное уравнение называется характеристическим. Обратно, если 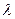корень характеристического уравнения, то система 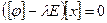имеет ненулевое решение, и значит, 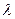является собственным числом. Тем самым доказана теорема.

Теорема 7.1. Корнями характеристического уравнения являются только собственные числа. Все собственные числа являются корнями характеристического уравнения.

Коэффициенты характеристического уравнения не зависят от выбора базиса. Действительно, матрицы линейного преобразования в разных базисах связаны уравнением 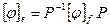, откуда .

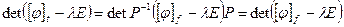Собственные векторы для собственного числа 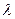принадлежат ядру линейного преобразования 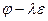. Подпространство 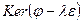называется корневым подпространством, соответствующим собственному числу .

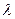Приведем простые факты.

Следствие 7.1. Линейное преобразование 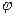линейного пространства 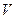над полем комплексных чисел имеет собственный вектор.

Доказательство. Над полем комплексных чисел характеристический многочлен имеет хотя бы один корень, а, значит, линейное преобразование имеет собственный вектор.

Следствие 7.2. Линейное преобразование 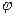линейного пространства 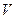над полем вещественных чисел имеет инвариантное подпространство размерности не выше 2.

Доказательство. Пусть 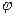- линейное преобразование пространства V над полем R. Если характеристический многочлен имеет вещественный корень, то утверждение леммы очевидно. На множестве 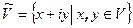определим операцию сложения и умножения на комплексное число . Множество 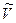относительно введенных операций сложения векторов и умножения на скаляр образует линейное пространство над C. Вектор x из V можно рассматривать как вектор из пространства 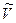, записанный в виде x+i0. Базис пространства V является базисом пространства 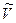, и, значит, размерности пространств V и 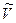совпадают. В пространстве 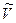рассмотрим линейное преобразование 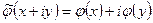. Пусть 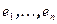- базис V. Тогда 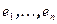- базис 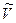и 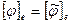. Пусть 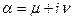- комплексное собственное число, а 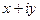- соответствующий собственный вектор линейного преобразования 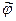. Тогда 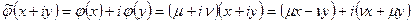, и, значит, 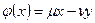, 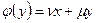. Линейная оболочка векторов x,y образует двумерное инвариантное подпространство.