Линейное преобразование и билинейные функции
Пусть V евклидово (унитарное) пространство. Обозначим через 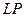 множество всех линейных преобразований пространства V, а через B множество билинейных функций, заданных на V. Если
множество всех линейных преобразований пространства V, а через B множество билинейных функций, заданных на V. Если 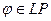 , то функция
, то функция 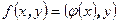 является билинейной. Таким образом, определено однозначное отображение множества линейных преобразований LP в множество билинейных функций B. Исследуем свойства этого отображения.
является билинейной. Таким образом, определено однозначное отображение множества линейных преобразований LP в множество билинейных функций B. Исследуем свойства этого отображения.
Свойство 8.1. Разные линейные преобразования отображаются в разные билинейные функции.
Доказательство проведем методом от противного. Пусть найдутся два разных линейных преобразования 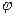 и
и 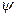 , которые отображаются в одну и ту же билинейную функцию. Тогда для любых векторов
, которые отображаются в одну и ту же билинейную функцию. Тогда для любых векторов 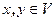 справедливо равенство
справедливо равенство 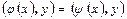 или
или 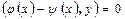 . Положим
. Положим 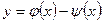 , тогда
, тогда  и
и  для любого вектора
для любого вектора 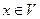 . Это означат, что линейные преобразования равны, что противоречит допущению.
. Это означат, что линейные преобразования равны, что противоречит допущению.
Свойство 8.2. Отображение линейных преобразований в билинейные функции взаимно однозначно.
Доказательство. Покажем, что для любой билинейной функции  существует линейное преобразование
существует линейное преобразование 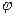 , что
, что 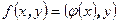 . Для каждого вектора x определим подпространство
. Для каждого вектора x определим подпространство 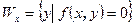 . Ортогональное дополнение к этому подпространству имеет размерность не выше 1. Действительно, если
. Ортогональное дополнение к этому подпространству имеет размерность не выше 1. Действительно, если 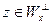 и
и 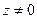 , то
, то 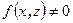 и для вектора
и для вектора 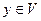 справедливо включение
справедливо включение 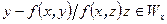 , и, значит
, и, значит 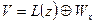 . Определим функцию
. Определим функцию 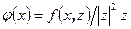 , где z – базис
, где z – базис 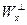 . Если
. Если 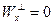 , то положим
, то положим 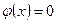 . Легко убедиться, что
. Легко убедиться, что 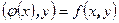 , и, значит функция
, и, значит функция 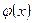 - линейное преобразование.
- линейное преобразование.
Аналогично, можно рассмотреть отображение LP на B, задаваемое формулой 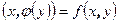 . Это отображение взаимно однозначно.
. Это отображение взаимно однозначно.
Линейное преобразование 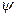 называется сопряженным преобразованием к
называется сопряженным преобразованием к 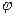 , если для любых векторов x,y из V справедливо равенство
, если для любых векторов x,y из V справедливо равенство  . Сопряженное преобразование к
. Сопряженное преобразование к 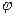 обозначают
обозначают 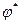 .
.
Дата добавления: 2016-05-25; просмотров: 882;
