Ортогональные преобразования

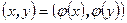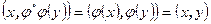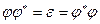Линейное преобразование называется ортогональным (унитарным) если оно сохраняет скалярное произведение, то есть . Из определения выводим или . Таким образом ортогональное преобразование является нормальным.

Свойство 8.6. Собственные числа ортогонального преобразования по модулю равны 1.

Доказательство. Пусть 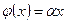, тогда 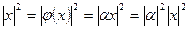, и, значит, .

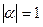Следствие 8.1. Ортогональное преобразование евклидова пространства, в некотором ортонормированном базисе, сводится к выполнению последовательности тождественных преобразований, симметрий и поворотов в координатных плоскостях.

Доказательство. Ортогональное преобразование нормально, следовательно, существует ортонормированный базис, в котором матрица линейного преобразования имеет блочно диагональный вид. Блоки первого порядка соответствуют вещественным собственным числам, а блоки второго порядка – комплексным числам. Так как собственные числа ортогонального преобразования по модулю равны 1, то по главной диагонали могут стоять либо 1, либо -1, либо блок второго порядка 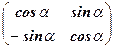. Для доказательства осталось заметить, что геометрический смысл указанных преобразований как раз и есть тождественные преобразования, симметрии и повороты в координатных плоскостях.