Приведение пары квадратичных форм

Рассмотрим задачу выбора базиса в котором пара квадратичных форм имеют диагональный вид. Не все пары квадратичных форм можно одновременно привести к диагональному виду, например, формы 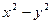и xy привести нельзя.

Первый способ

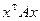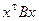Пусть даны квадратичные формы и , причем квадратичная форма 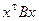- положительно определена. Тогда введем скалярное произведение 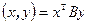и найдем ортонормированный базис, а затем приведем первую квадратичную форму к главным осям. Поскольку ортогональное преобразование не меняет скалярное произведение, то обе квадратичные формы будут приведены к каноническому виду.

Пучок матриц

Пусть даны квадратичные формы 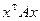и 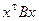. Рассмотрим пучок квадратичных форм 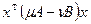. Если квадратичные формы 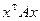и 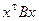заменой координат x=Py приводятся к каноническому виду, то все формы из пучка 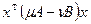приводятся к каноническому виду этой же заменой координат. Пусть 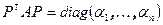и 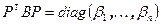, тогда 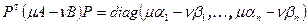. Из последнего равенства выводим 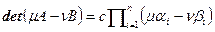, то есть многочлен 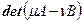раскладывается на линейные множители над полем вещественных чисел. Из равенства 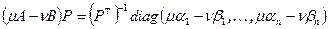выводим, что i-ый столбец матрицы P удовлетворяет однородной системе уравнений 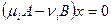. Таким образом, получается следующий алгоритм приведения пары квадратичных форм к нормальному виду.

1. Раскладываем многочлен 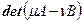на линейные множители. Если разложения не существует, то искомой замены координат не существует.
2. Для каждого линейного множителя 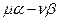многочлена 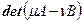находим базис подпространства 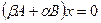. Если размерность подпространства меньше кратности множителя, то искомой замены координат не существует. В противном случае, будет построен базис, в котором квадратичные формы имеют нормальный вид.

Для обоснования этого подхода требуется показать, что объединение линейно независимых систем векторов, соответствующих разным линейным множителям, образует линейно независимую систему. Доказательство проводится также как и для собственных векторов.

Приведение квадрики ортогональным преобразованием. Ортогональные инварианты и полуинварианты.

Рассмотрим задачу упрощения уравнения квадрики с использованием ортогональным преобразованием системы координат. Отметим, что при ортогональной замене координат сохраняются метрические характеристики.

Опишем алгоритм приведения квадрики 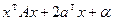к простейшему виду ортогональным преобразованием.

1. Приводим квадратичную форму 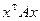к главным осям ортогональным преобразованием 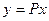. В результате получим уравнение квадрики 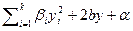, где 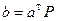, k – ранг матрицы A, а 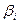- ее ненулевые собственные числа.
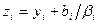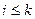2. Сдвигом начала координат при и 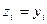при i>k приведем квадрику к виду 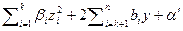, где 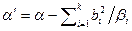. Если 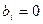при i>k, то конец, а иначе перейдем на следующий шаг.
3. Положим 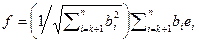. Система векторов 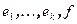- ортонормированная. Дополним ее до ортонормированного базиса всего пространства. Пусть T – матрица перехода к новому базису. Сделаем замену переменных 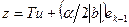. Очевидно, сделанная замена является ортогональной. В новой системе координат уравнение квадрики .

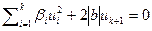Оформим доказанное выше в виде теоремы.

Теорема 9.2. Ортогональным преобразованием, сдвигом начала координат и умножением на ненулевое число уравнение квадрики приводится к одному из следующих четырех видов , , , .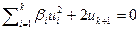

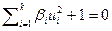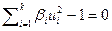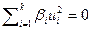Обозначим через 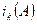сумму всех главных миноров k-го порядка матрицы A. Величина 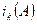является коэффициентом характеристического многочлена 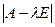при .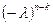

Пусть квадрика 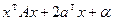ортогональным преобразованием x=h+Ty приводится к виду 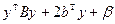, где 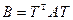, , 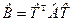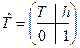. Поскольку T ортогональная матрица, то 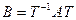, и, значит, 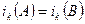, где k=1,…,n. Кроме того, 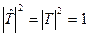, и, следовательно, 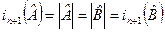. Тем самым установлен следующий факт.

Свойство 9.1 При ортогональном преобразовании не меняются следующие величины 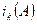, где k=1,…,n, и 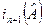, которые называются ортогональными инвариантами квадрики.

К сожалению, ортогональные инварианты не всегда позволяют установить простейший тип квадрики.

Свойство 9.2. Пусть 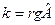и 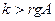, тогда 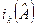не меняется при ортогональном преобразовании.

Доказательство. При ортогональном преобразовании (без сдвига) величины 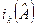не меняются. Пусть квадратичная форма 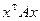приводится к главным осям ортогональной заменой координат 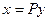. Пусть 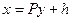- ортогональное преобразование квадрики. Поскольку 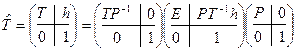, то для доказательства утверждения достаточно рассмотреть случай, когда 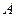- диагональная матрица и преобразование заключается в сдвиге на вектор h начала координат. Если 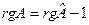, то 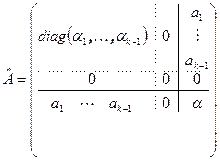. В этой матрице единственный минор k порядка, не содержащий нулевых строк, определитель которого не зависит от сдвига. Следовательно, утверждение в данном случае доказано. Пусть 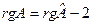, тогда 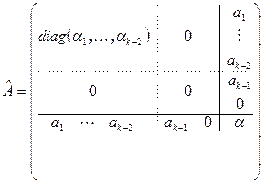. В этой матрице единственный минор k порядка, не содержащий нулевых строк, определитель которого не зависит от сдвига. Следовательно, утверждение и в данном случае доказано.

Величины 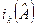называются полуинвариантами ортогонального преобразования.

Набор инвариантов и полуинвариантов квадрики позволяет однозначно установить простейшее уравнение квадрики.