Полярное разложение

Самосопряженное преобразование 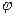называется положительно определенным, если .

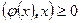Следствие 8.3. Все собственные числа положительно определенного самосопряженного линейного преобразования неотрицательны.

Доказательство. Пусть 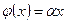, тогда 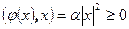, и, значит, .

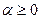Теорема 8.3. (извлечение корня) Для положительно определенного самосопряженного линейного преобразования 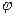существует единственное положительно определенное самосопряженное преобразование 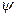, что .

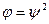Доказательство. Пусть 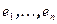- ортонормированный базис линейного пространства, в котором матрица 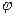- диагональная. Пусть 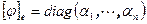. Все числа стоящие на главной диагонали неотрицательны. Положим 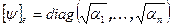. Легко убедиться, что линейное преобразование 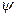является положительно определенным самосопряженным преобразованием и 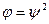. Единственность очевидна.

Теорема 8.4 (полярное разложение) Любое линейное преобразование 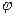можно представить в виде произведения самосопряженного положительно определенного линейного преобразования 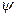и ортогонального преобразования 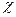. Если 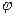- невырожденное, то представление единственно. Разложение 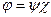называется правым, а разложение 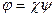- левым.

Доказательство. Преобразование 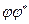является самосопряженным и положительно определенным. Построим ортонормированный базис 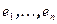преобразования 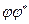, при этом расположим собственные векторы, соответствующие нулевому собственному значению в конце базиса. Пусть 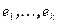- собственные векторы с не нулевыми собственными значениями, а 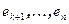- собственные векторы с нулевым собственным значением. Матрица 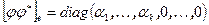- диагональная, поэтому первые k строк матрицы 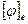образуют ортогональную систему, а остальные равны 0. Длина j строки равна 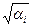. Обозначим через 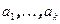первые k строк матрицы 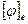и дополним ортонормированную систему векторов 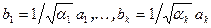векторами 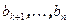до ортонормированного базиса всего пространства. Обозначим через 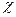ортогональное преобразование, матрица которого в базисе 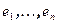образована строками 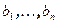, а через 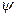- положительно определенное самосопряженное преобразование, матрица которого в базисе 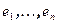диагональная и равна 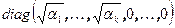. Легко убедиться, что .

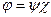Для построения левого разложения достаточно найти правое разложение для сопряженного преобразования.

Поскольку 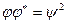, то преобразование 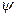определяется единственным образом. Если преобразование 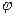- невырожденное, то преобразование 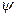невырожденное, и, значит, 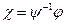определяется единственным образом.