Вычисление суммы ряда. Разложение функций в ряды.

Для вычисления суммы ряда в системе MATLAB используется функция symsum, синтаксис обращения к которой имеет вид:

symsum(func [, var, a, b])

где func – символьное выражение, обозначающее общий член суммы числового ряда, зависящий от переменной var, которая, в свою очередь, может принимать значения от a до b.

Пусть требуется вычислить суммы ряда

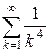и .

И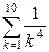меем:

>> syms x k

>> s1=symsum(1/k^4,1,inf)

s1 =

pi^4/90

>> s2=symsum(1/k^4,1,10)

s2 =

43635917056897/40327580160000

Приведем теперь пример расходящегося ряда

,

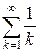при попытке вычисления суммы элементов которого будем иметь:

>> syms x k

>> s=symsum(1/k,1,inf)

s =

Inf

Для формирования ряда Маклорена (являющегося частным случаем ряда Тейлора) символьной функции func до n-го члена (если параметр n отсутствует, то по умолчанию до шестого) следует использовать функцию

taylor(func [, n])

Пусть, например, требуется разложить в ряд Маклорена функцию

.

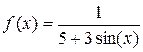Имеем:

>> syms x

>> f=1/(5+3*sin(x));

>> T=taylor(f)

T =

(631*x^5)/125000 + (6*x^4)/3125 - (29*x^3)/1250 + (9*x^2)/125 - (3*x)/25 + 1/5

Функция taylor(func, var [, a]) возвращает разложение в ряд Тейлора для символьной функции func относительно переменной var окрестности точки a.

Пусть, например, требуется разложить в ряд Тейлора (вывести первые три члена) в окрестности точки 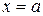функцию

.

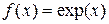Имеем:

>> syms x a

>> taylor(exp(x),x,a)

ans =

exp(a) + (exp(a)*(a - x)^2)/2 - (exp(a)*(a - x)^3)/6 + (exp(a)*(a - x)^4)/24 - (exp(a)*(a - x)^5)/120 - exp(a)*(a - x)