Вычисление линейных рекуррентных последовательностей
Последовательность 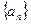 называется линейной рекуррентной, если существуют такие коэффициенты
называется линейной рекуррентной, если существуют такие коэффициенты 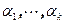 , что для любого n справедливо равенство
, что для любого n справедливо равенство 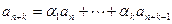 . Для задания линейной рекуррентной последовательности, кроме ее коэффициентов, необходимо знать первые k членов
. Для задания линейной рекуррентной последовательности, кроме ее коэффициентов, необходимо знать первые k членов 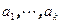 , которые называются начальными условиями. Рассмотрим задачу выражения n-го члена последовательности через его номер и начальные условия.
, которые называются начальными условиями. Рассмотрим задачу выражения n-го члена последовательности через его номер и начальные условия.
Обозначим через 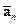 вектор столбец, состоящий из k компонент
вектор столбец, состоящий из k компонент 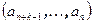 , через
, через 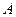 — матрицу размерами
— матрицу размерами 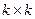 вида
вида 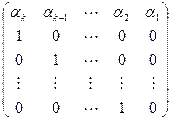 . По правилу перемножения матриц имеем:
. По правилу перемножения матриц имеем: 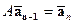 . Многократным применением полученной формулы выводим
. Многократным применением полученной формулы выводим 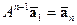 . Задача вычисления n-го члена последовательности свелась, тем самым, к вычислению матрицы
. Задача вычисления n-го члена последовательности свелась, тем самым, к вычислению матрицы 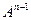 .
.
Характеристический многочлен 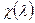 матрицы А равен
матрицы А равен 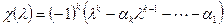 . Разделим многочлен
. Разделим многочлен 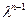 на
на 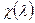 с остатком. Пусть
с остатком. Пусть 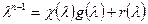 , где
, где 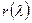 - остаток от деления. Подставив вместо λ матрицу А, получим
- остаток от деления. Подставив вместо λ матрицу А, получим 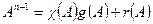 . По теореме Гамильтона-Кэли каждая матрица является корнем своего характеристического уравнения, то есть
. По теореме Гамильтона-Кэли каждая матрица является корнем своего характеристического уравнения, то есть 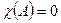 , где 0 - нулевая матрица. Таким образом,
, где 0 - нулевая матрица. Таким образом, 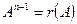 , и задача вычисления
, и задача вычисления 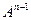 свелась к вычислению многочлена r(λ).
свелась к вычислению многочлена r(λ).
Разложим многочлен 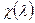 на линейные множители
на линейные множители 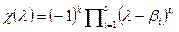 , где
, где 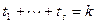 . Для каждого неотрицательного j строго меньшего
. Для каждого неотрицательного j строго меньшего 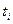 справедливо равенство
справедливо равенство 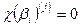 , где
, где 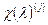 - j-ая производная характеристического многочлена. Продифференцировав j раз равенство
- j-ая производная характеристического многочлена. Продифференцировав j раз равенство 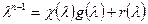 и, подставив в него
и, подставив в него 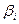 , получим
, получим 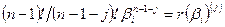 . Этими условиями многочлен r(λ) степени k-1 определяется однозначно. В литературе задача вычисления многочлена по таким условиям носит название «интерполяционный многочлен Лагранжа-Сильвестра».
. Этими условиями многочлен r(λ) степени k-1 определяется однозначно. В литературе задача вычисления многочлена по таким условиям носит название «интерполяционный многочлен Лагранжа-Сильвестра».
В качестве примера вычислим n-ый член линейной рекуррентной последовательности 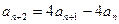 , где
, где 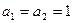 . Положим
. Положим 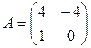 . Характеристический многочлен равен
. Характеристический многочлен равен 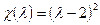 . Остаток от деления
. Остаток от деления 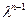 на
на 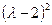 удовлетворяет соотношениям
удовлетворяет соотношениям 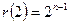 и
и 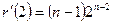 . Единственный многочлен первой степени, удовлетворяющий этим условиям, равен
. Единственный многочлен первой степени, удовлетворяющий этим условиям, равен 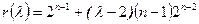 . Таким образом,
. Таким образом, 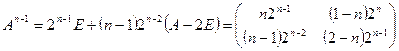 и
и 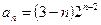 .
.
Дата добавления: 2016-05-25; просмотров: 953;
