Приведение квадратичных форм к главным осям.

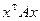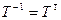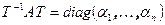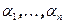Рассмотрим квадратичную форму . Матрица A является симметричной. Линейное преобразование, заданное матрицей A, является самосопряженным и для этого преобразования существует ортонормированный базис из собственных векторов. Другими словами, найдется ортогональная матрица T ( ), что , где - собственные числа A. Поскольку 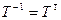, то квадратичная форма 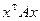ортогональной заменой 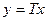переходит в форму 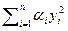. Приведение квадратичной формы к каноническому виду ортогональным преобразованием называется приведением к главным осям. Полученный факт оформим в виде теоремы.

Теорема 9.1. Квадратичная форма 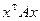при помощи ортогонального преобразования всегда может быть приведена к канонической форм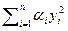е , де 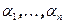- собственные числа A.

Отметим, что для квадратичной формы выполняется закон инерции. Следовательно, используя теорему Якоби, можно определить число положительных и число отрицательных собственных значений. Собственные значения матриц A и A-tE отличаются на t, поэтому, определяя число положительных и отрицательных собственных значений матрицы A-tE, мы, тем самым, определим количество собственных значений матрицы A меньших t. Выбирая различные t можно найти собственные числа с любой точностью.