Разложение булевых функций по переменным.

Алгебра Буля

Одна и та же логическая функция может быть задана формулами, включающими различные наборы логических операций. Существуют наборы логических операций (унарных и бинарных), с помощью которых можно выразить любые другие логические функции. Такие наборы называются функционально полными системами.

Наиболее хорошо изученной является полная система булевых функций 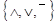. Формулы, содержащие кроме переменных (и скобок) только знаки функций 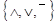, называются булевыми.

Алгебра, основным множеством которой является все множество логических функций, а операциями – дизъюнкция, конъюнкция и отрицание, называется булевой алгеброй логических функций (алгеброй Буля).

Элементами основного множества булевой алгебры являются не формулы, а классы эквивалентности формул, т.е. классы формул, реализующих одну и ту же функцию.

Основные эквивалентные соотношения в булевой алгебре представлены в таблице 5.

Таблица 5

Основные аксиомы алгебры Буля

Аксиомы отрицания
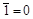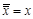
Аксиомы конъюнкции и дизъюнкции
Аксиомы конъюнкции	Аксиомы дизъюнкции	Название аксиомы
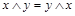
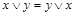
		коммутативность
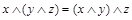
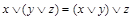
		ассоциативность
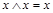
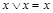
		идемпотентность
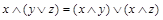
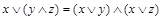
		дистрибутивность
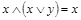
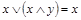
		поглощение
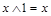
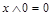
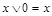
		аксиомы 0 и 1
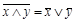
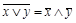
		законы де Моргана
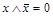
аксиома противоречия	аксиома "исключенного третьего":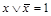

Теорема: Любая представленная формулой логическая функция может быть представлена булевой формулой, то есть как суперпозиция функций конъюнкции, дизъюнкции, отрицания.

Для доказательства этой теоремы достаточно предложить любой способ построения булевой формулы. Пусть логическая функция задана некоторой формулой (не являющейся булевой), тогда с помощью эквивалентных преобразований (используя равносильности I, II и III групп (см. п. 4)) нужно заменить все логические операции на булевы операции.

Булевых формул для каждой логической функции бесконечно много, так как любое эквивалентное преобразование дает новую формулу той же логической функции.

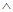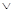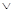Принцип двойственности для булевых формул: Двойственная к булевой формуле может быть получена заменой констант 0 на 1, 1 на 0, на , на 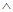и сохранением структуры формулы (т.е. соответствующего порядка действий).

Например, 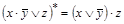. Скобка в правой части поставлена для сохранения структуры формулы.

Теорема: Булева алгебра логики высказываний изоморфна булевой алгебре множеств.

Такой изоморфизм можно установить, если под элементами 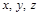(см. табл. 5) понимать множества, под операциями " 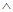", " ", " 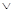" – пересечение, объединение, дополнение множеств, под знаком равенства – знак равенства множеств, под единицей понимать универсальное множество, под нулем – пустое множество.

Последняя теорема позволяет заменить теоретико-множественные операции (объединение, пересечение, дополнение) над системой множеств поразрядными логическими операциями над двоичными векторами. Эта замена часто используется в системах программирования.

Разложение булевых функций по переменным.