Аналитическое выражение проективного преобразования плоскости.

Проективные преобразования плоскости и прямой, свойства.

Аналитическое выражение проективных преобразований.

Гомологии. Инволюция

Рассмотрим на проективной плоскости 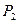два проективных репера 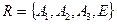и .

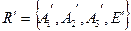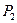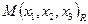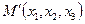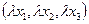Определение 6.1. Преобразование проективной плоскости , которое каждой точке ставит в соответствие точку, имеющую такие же координаты или , где 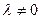, относительно репера 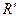, называется проективным преобразованием плоскости.

Свойства проективного преобразования 6.2.

6.2.1. Всякое проективное преобразование плоскости переводит прямую в прямую. (Следует, что всякое проективное преобразование плоскости сохраняет коллинеарность точек. Поэтому проективное преобразование плоскости называеют еще коллинеацией).

6.2.2. Существует единственное проективное преобразование, которое любую упорядоченную четверку точек общего положения 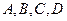переводит в любую наперед заданную упорядоченную четверку точек .

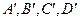6.2.3. Всякое проективное преобразование плоскости сохраняет сложное отношение четырех точек прямой.

Аналитическое выражение проективного преобразования плоскости.

Пусть дано проективное преобразование 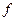, заданное парой реперов 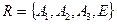и 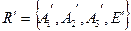. Точка 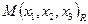- произвольная точка в репере 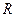, точка 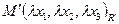- образ точки 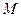при преобразовании .

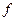Пусть 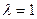, тогда 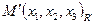. Обозначим координаты точки 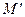относительно репера 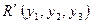. Найдем связь координат точки 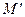в двух проективных реперах: для этого воспользуемся формулами перехода от репера 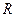к реперу 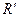(лекция 2), причем 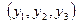- новые координаты точки 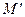, а

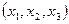- старые координаты этой точки. Получим:

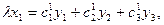
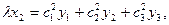
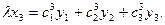
Это и есть формулы проективного преобразования плоскости.

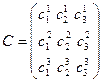- матрица проективных преобразований. Определитель матрицы 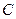отличен от нуля, так как точки 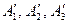не лежат на одной прямой.

На расширенной аффинной (или евклидовой ) плоскости можно ввести неоднородные координаты. Воспользовавшись формулами 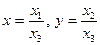, имеем: 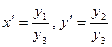. Тогда формулы проективных преобразований плоскости в неоднородных координатах примут следующий вид: , .

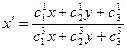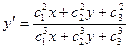Пусть 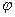- проективное отображение прямой 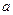на прямую 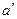. 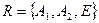- проективный репер на прямой 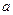, 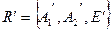- проективный репер на прямой .

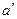Определение 6.3.Отображение 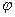прямой 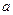на прямую 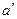, которое каждой точке прямой 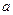, имеющей в репере 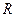координаты 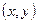, ставит в соответствие точку 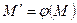, принадлежащую прямой 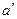с теми же координатами 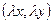в репере 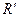, называется проективным.

Если 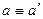, то 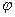- проективное преобразование, то есть проективное отображение прямой на себя также называется проективным преобразованием.

По аналогии с нахождением формул проективных преобразований плоскости можно получить формулы проективных преобразований прямой: 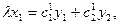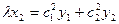. Определитель матрицы, составленной из коэффициентов правых частей данных формул проективных преобразований на прямой, отличен от нуля. На расширенной аффинной (или евклидовой) прямой, введя неоднородные координаты, имеем следующую формулу: .

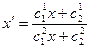Определение 6.4.Проективное преобразование прямой называется инволюцией, если оно совпадает со своим обратным преобразованием.