Свойства инволюций 6.5.

6.5.1. Инволюция может иметь либо две инвариантные точки, либо ни одной.

Если инволюция имеет две инвариантные точки, то она называется гиперболической; если инволюция не имеет инвариантных точек, то она называется эллиптической.

6.5.2. Если и - и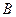нвариантные точки гипербоинволюции, то они гармонически разделяют любую пару соответствующих при инволюции точек этой прямой.

Теорема 6.6. (признак инволюции) Если проективное преобразование прямой какую-нибудь точку прямой переводит в точку 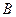, а точку 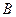в точку , то оно является инволюцией.

Инвариантные точки и инвариантные прямые

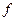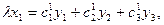
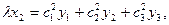
Пусть дано проективное преобразование плоскости: 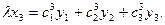Определитель матрицы преобразований отличен от нуля.

Определение 6.7.Точка 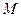проективной плоскости 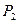называется инвариантной точкой проективного преобразования 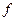, если ее образ совпадает с точкой .

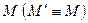Найдем характеристическое уравнение для нахождения инвариантных точек. Пусть 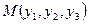, тогда, если 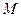-инвариантная точка, то 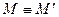и 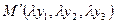. В формулах проективных преобразований плоскости заменим

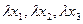на :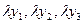

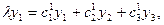
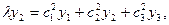
Выполнив преобразования, получим: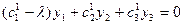

.

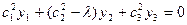
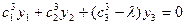Система уравнений однородна, имеет ненулевые решения, если ее определитель равен нулю: 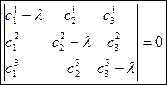- характеристическое уравнение для нахождения инвариантных точек. Оно имеет по крайней мере один действительный корень. Решая, находим 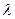, которое позволяет найти координаты инвариантной точки. Таким образом, всякое проективное преобразование плоскости имеет по крайней мере одну инвариантную точку.

Определение 6.8. Прямая 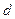называется инвариантной прямой проективного преобразования 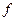, если ее образ 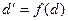совпадает с прямой 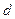. (Образ любой точки 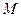прямой 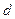принадлежит этой же прямой ).

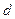Пусть прямая 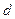задана уравнением 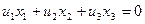и точка прямой 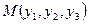. При проективном преобразовании 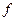точка 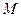переходит в точку 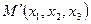. Так как прямая 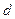инвариантная, то точка 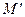принадлежит прямой 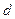, и координаты этой точки удовлетворяют ее уравнению: (*).

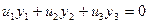Подставим в уравнение (*) вместо 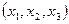их выражения из формул проективных преобразований при 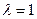. Получим:

(**)

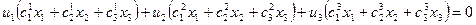Полученное уравнение (**) является уравнением прямой 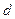, так как она инвариантная, то есть уравнение (**) должно совпадать с уравнением 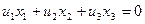. Тогда коэффициенты при неизвестных будут пропорциональными.

.

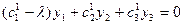
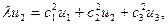
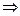
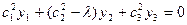
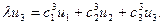
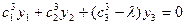Так как 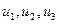не равны нулю одновременно, то определитель системы равен нулю. Итак, всякое проективное преобразование имеет по крайней мере одну инвариантную прямую.

Гомология

Определение 6.9. Проективное преобразование плоскости, которое имеет прямую инвариантных точек, а значит, и пучок инвариантных прямых называется гомологией.

Определение 6.10.Центр пучка инвариантных прямых называется центром гомологии; прямая инвариантных точек называется осью гомологии.

Гомология задается центром; осью; парой соответственных точек.

Виды гомологии:

ü гиперболическая (центр не лежит на оси гомологии)

ü параболическая (центр лежит на оси гомологии).