Возведение в степень комплексного числа.

.

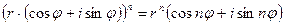Важный частный случай при r= 1: 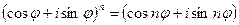- формула Муавра. По этой формуле легко получать тригонометрические формулы кратных аргументов.

Например:пусть n= 3

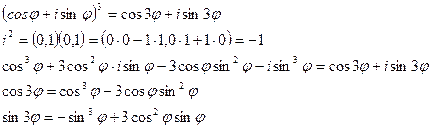
Извлечение корней из комплексных чисел.

Операция извлечения корня n-й степени из комплексного числа определяется как операция, обратная по отношению к возведению в n-ю степень.

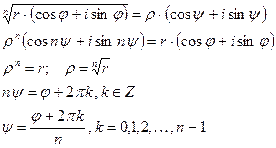
Всего имеется nразличных комплексных корней.

.

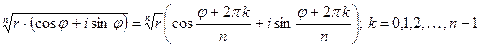Пример:найдем корень из (-2); .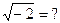

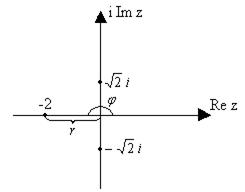
Представим это число в тригонометрической форме

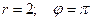
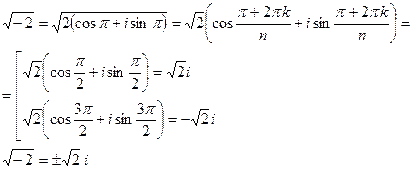
Лекция 12 Обыкновенные дифференциальные уравнения

(Тема 4.2)

План лекции

Понятие дифференциального уравнения.

Общее и частное решение.

Уравнение с разделяющимися переменными.

Линейные уравнения первого порядка.

Уравнения второго порядка, допускающие понижения порядка.

Линейные однородные уравнения второго порядка с постоянными коэффициентами.

Определение: дифференциальным уравнением будем называть уравнение, связывающее между собой независимую переменную х, зависимую переменную у и ее производные: 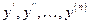, т.е. уравнение вида: .

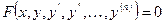Определение: решением дифференциальные уравнения будем называть функцию 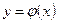, после подстановки которой в исходное дифференциальное уравнение, оно превращается в верное равенство, т.е.:

.

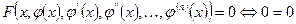Определение: общим решением дифференциального уравнения будем называть решение, содержащее произвольные постоянные 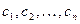, количество которых совпадает с порядком старшей производной, фигурирующей в данном дифференциальном уравнении, если количество этих постоянных не может быть сокращено с помощью замен переменных.

Определение: порядком дифференциального уравнения называют порядок старшей производной.

Пример: рассмотрим дифференциальное уравнение 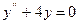. Это дифференциальное уравнение второго порядка. Проверим, что функция 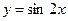является его решением:

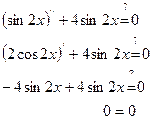
Замечание: легко убедиться, что решением также будет функция 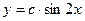, где с – любая постоянная величина.

Также легко убедиться, что решением будет и функция 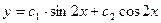, а поскольку произвольных постоянных две, то это общее решение.

Определение: частным решением дифференциального уравнения называется решение, которое получается из общего при конкретном выборе значений произвольных постоянных.

Определение: в тех случаях, когда не удается явно выразить у через независимую переменную х и произвольные постоянные 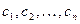, находят общий интеграл дифференциального уравнения в виде: .

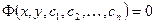Если известен общий интеграл, то исключая произвольные постоянные 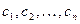из системы уравнений:

,

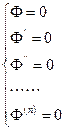получим исходное дифференциальное уравнение, т.е. по общему интегралу можно узнать, какому дифференциальному уравнению он удовлетворяет.

Пример: найти дифференциальное уравнение по известному общему решению.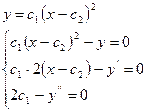

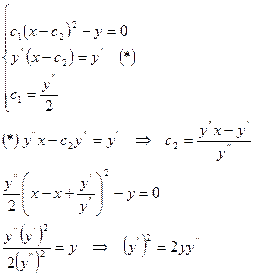
Для дифференциального уравнения 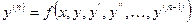зададим значения функции и всех производных. Вплоть до производной (n-1)-го порядка в некоторой точке х₀, тогда получим дифференциальное уравнение с начальными условиями:

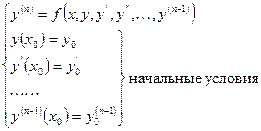
Определение: задачей Коши называется задача о нахождении частного решения дифференциального уравнения, удовлетворяющего начальным условиям. Если известно общее решение 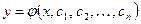, то конкретные значения произвольных постоянных находятся из решения системы:

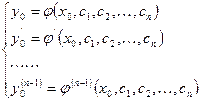
График решения дифференциального уравнения называют интегральной кривой.