Замена переменных в двойном интеграле
Расмотрим двойной интеграл вида 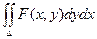 , где переменная х изменяется в пределах от a до b, а переменная у – от j1(x) до j2(х). Положим х = f(u, v); y = j(u, v)
, где переменная х изменяется в пределах от a до b, а переменная у – от j1(x) до j2(х). Положим х = f(u, v); y = j(u, v)
Тогда dx = 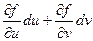 ; dy =
; dy = 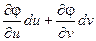 ;
;
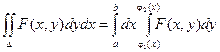
т.к. при первом интегрировании переменная х принимается за постоянную, то dx = 0.
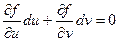 , т.е.
, т.е. 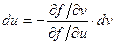
пожставляя это выражение в записанное выше соотношение для dy, получаем:
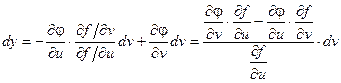
Выражение 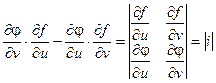 называется определителем Якобиили Якобианомфункций f(u, v) и j(u, v).
называется определителем Якобиили Якобианомфункций f(u, v) и j(u, v).
(Якоби Карл Густав Якоб – (1804-1851) – немецкий математик)
Тогда 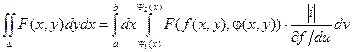
Т.к. при первом интегрировании приведенное выше выражение для dx принимает вид 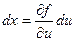 ( при первом интегрировании полагаем v = const, dv = 0), то при изменении порядка интегрирования, получаем соотношение:
( при первом интегрировании полагаем v = const, dv = 0), то при изменении порядка интегрирования, получаем соотношение: 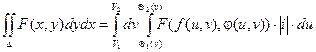
Вычисление двойного интеграла 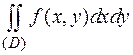 сводится к вычислению одного или двух двукратных интегралов вида
сводится к вычислению одного или двух двукратных интегралов вида 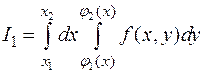
Или 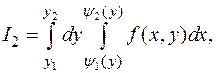 каждый из которых есть результат последовательного вычисления двух обыкновенных определенных интегралов. При этом значение двойного интеграла не зависит от порядка интегрирования.
каждый из которых есть результат последовательного вычисления двух обыкновенных определенных интегралов. При этом значение двойного интеграла не зависит от порядка интегрирования.
Рассмотрим пример. Вычислить двойной интеграл 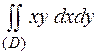 , если область D – треугольник, ограниченный прямыми х=0, 2у-х=0, х+у=3.
, если область D – треугольник, ограниченный прямыми х=0, 2у-х=0, х+у=3.
Если в начале интегрировать по у, а затем по х, то двойной интеграл по области D выражается одним двукратным интегралом
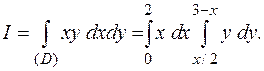
Вычисляя двукратный интеграл, получим:
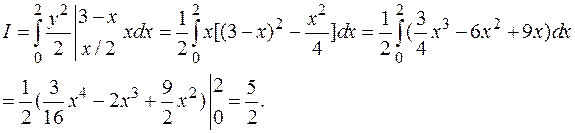
Если интегрировать в другом порядке – сначала по х, а затем по у, необходимо разбить область интегрирования прямой у=1 на две части, так как правая линия границы состоит из двух участков, которые имеют различные уравнения: х=2у и х=3-у. Вследствие этого вычисления несколько усложняются:
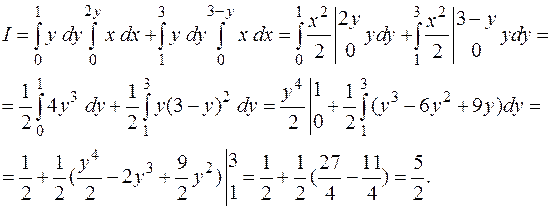
Дата добавления: 2016-06-24; просмотров: 1907;
