Лекция 11 Основы теории комплексных чисел
(Тема 4.1.)
План лекции
Понятие комплексного числа.
Изображение на плоскости и операции над комплексными числами.
Алгебраическая показательная и тригонометрическая форма комплексного числа.
Определение:комплексным числом будем называть упорядоченную пару чисел (a; b), упорядоченную в том смысле, что нам известно, какое из чисел первое, а какое второе.
Число (а, 0) = а является вещественным или действительным числом а.
Равенство двух комплексных чисел (a, b) = (c, d) означает, что 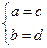 .
.
Для комплексных чисел вводится операция сложенияпо следующему правилу:
(a, b) + (c, d) = (a+ c, b+ d).
Для операции сложения комплексных чисел справедливы следующие свойства:
1. От перестановки слагаемых сумма не меняется: (a, b) + (c, d) = (c, d) + (a, b)
2. Для операции сложения выполняется сочетательный закон: 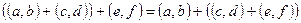 .
.
Для комплексных чисел вводится операция вычитания, как операция, обратная к сложению, а именно: разностью комплексных чисел (a, b) и (c, d) называется комплексное число (х, у), которое после сложения с числом (c, d) дает число (a, b).
(a, b) – (c, d) = (x, y); (x, y) + (c, d) = (a, b) – выполним сложение: (x+ c, y+ d) = (a, b)
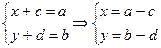 . Таким образом: (a, b) – (c, d) = (a– c, b– d).
. Таким образом: (a, b) – (c, d) = (a– c, b– d).
Для комплексных чисел вводится операция умноженияпо следующему правилу:
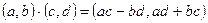 .
.
Для операции умножения выполняются следующие свойства:
1. Произведение не зависит от порядка сомножителей: 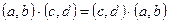 .
.
2. Выполняется сочетательный закон: 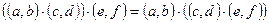 .
.
3. Выполняется сочетательный закон: 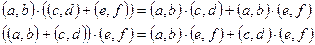 .
.
Утверждение:если известно, что 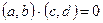 , причем
, причем 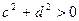 , то (a, b) = (0, 0).
, то (a, b) = (0, 0).
Доказательство:
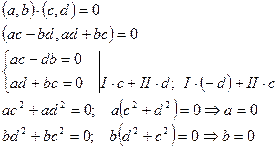
Для комплексных чисел вводится операция делениякак операция, обратная по отношению к операции умножения, а именно: частным от деления комплексных чисел (a, b) и (c, d), где 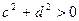 , называется комплексное число (х, у), такое, что его произведение с числом (c, d) дает число (a, b).
, называется комплексное число (х, у), такое, что его произведение с числом (c, d) дает число (a, b).
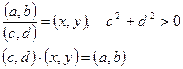
Нетрудно показать, что частное находится по следующему правилу:
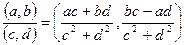
Определение:комплексные числа (0, b) называются чисто мнимыми, обозначаются: 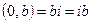 .
.
Любое комплексное число может быть представлено в следующей форме: 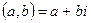 .
.
Доказательство: 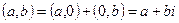 .
.
Число 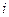 , которое называется мнимой единицей, мы получаем при b= 1,
, которое называется мнимой единицей, мы получаем при b= 1, 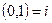 ,
, 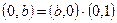 .
.
Дата добавления: 2016-06-24; просмотров: 1257;
