Коды, получаемые с помощью матриц Адамара.

Матрицей Адамара называется ортогональная квадратная матрица размерности n x n, элементами которой являются действительные числа +1 и -1. Ортогональной называется матрица, строки которой являются взаимно ортогональными векторами.

Теорема 1. Если существует матрица Адамара размерности n x n, то существует двоичный код из n символов, образованный 2n векторами, с минимальным расстоянием, равным n/2 (не обязательно линейный код).

Доказательство: Пусть H – матрица Адамара. Код строиться следующим образом. Берется совокупность из 2n векторов v₁,v₂,…,v_n,-v₁v₂,…,-v_n, где v₁,v₂,…,-v_n и заменяются в каждом из векторов все +1 на 0, а все -1 на 1. Тогда получается совокупность 2n двоичных векторов длины n. Поскольку соответствующие компоненты векторов v_i и –v_i различны, то расстояние между векторами v_i и –v_i равно n. Поскольку векторы ±vi и ±v_j ортогональны, если i≠j, то они должны совпадать в половине компонент и отличаться друг от друга в остальных компонентах, так что соответствующие двоичные векторы находятся на расстоянии n/2.

Теорема 2. Если H – матрица Адамара размерности n x n, то матрица

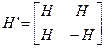
является матрицей Адамара размерности 2n x 2n.

Доказательство: Очевидно, что матрица H’ является квадратной матрицей с элементами, равными +1 или -1. Скалярное произведение j-ой и (n+j)-й строк (j≤n) равно:

.

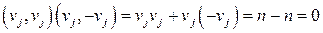Для любых других комбинаций строк

(v_i, ±v_i)(v_j, ±v_j)=v_iv_j±v_iv_j=0±0=0.

Следовательно, H’ – ортогональная матрица.

Пример:

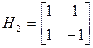
Многократно применяя теорему 2 можно построить матрицу Адамара размерности 2(^m) x 2(^m) для любого целого положительного m. Соответствующий ей код совпадает с кодом Рида-Маллера первого порядка. Для других значений n двоичные коды, получаемые с помощью матриц Адамара, не могу быть групповыми кодами, поскольку число их кодовых векторов не является степенью двойки.