Идеалы и классы вычетов целых чисел.

Если r,s и t – целые числа и rs=t, то говорят, что t делится на r или что r является делителем числа t. Целое число p≥1, которое делится только на ±p и на ±1 называется простым. Наибольшим общим делителем (НОД) двух целых чисел называется наибольшее положительное число, являющееся делителем обоих этих чисел. Говорят, что два целых числа взаимно просты, если их наибольший делитель равен 1.

Для любой пары целых чисел s и d существует единственная пара целых чисел q (частное) и r (остаток), таких, что:

(i.1) 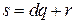, где

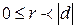
Общий делитель d двух целых чисел r и s всегда можно представить в виде:

(i.2) 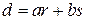, где a и b – целые числа.

Алгоритм Евклида.

Пусть даны числа 973 и 301. НОД: d-?

973 = 3 x 301 + 70

301 = 4 x 70 + 21

70 = 3 x 21 + 7

21 = 3 x 7 + 0

Так как число d является делителем 973 и 301, то оно должно быть делителем и остатка 70. Т.к. d – делитель 301 и 70, оно является делителем 21. Т.к. d – делитель 70 и 21, то оно является делителем 7. С другой стороны, 7 является делителем 21, 70, 301 и 973. Поэтому d=7.

7 = 70 - 3 x 21 = 70 – 3 x (301 – 4 x 70) = -3 x 301 + 13 x 70 = -3 x 301 + 13 x (973-3 x 301) = 13 x 973 – 42 x 301.

Теорема 1: Совокупность целых чисел образует идеал тогда и только тогда, когда она состоит из всех чисел, кратных некоторому целому числу.

Доказательство: Пусть r – наименьшее целое положительное число в идеале и s – любое другое целое число, принадлежащее идеалу. Тогда НОД этих чисел d принадлежит идеалу, потому что по определению идеала оба слагаемых в правой части соотношения (i.2) принадлежат идеалу, и, следовательно, их сумма также принадлежит идеалу. Так как r – наименьшее положительно число в идеале, то r≤d. Поскольку r делится на d, то d≤r. Следовательно, r=d и s делится на r, т.е. на r делиться любое целое число, принадлежащее идеалу. Наконец, любое число, кратное r, принадлежит идеалу по определению идеала.

Идеал, который состоит из всех элементов, кратных одному из элементов кольца, называется главным идеалом, а кольцо, в котором каждый идеал главный, называется кольцом главных идеалов.

Идеал, который состоит из всех чисел, кратных положительному целому числу m, обозначается через (m). Кольцо классов вычетов, образованное классами вычетов по идеалу (m), называется кольцом целых чисел по модулю m.

Теорема 2: Каждый класс вычетов по модулю m содержит либо 0, либо целое положительное число, меньшее m. Нуль является элементом идеала, а все остальные целые положительные числа меньше m, принадлежат различным классам вычетов.

Доказательство: Если s – любой элемент некоторого класса вычетов, то поскольку 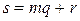, r – принадлежит тому же самому классу вычетов и 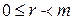. Если r и s принадлежат одному и тому же классу вычетов, то разность r-s является элементом идеала, и, следовательно, кратна m. Если r≠s то, очевидно, эти числа не могут быть оба меньше чем m и неотрицательны.

Теорема 3: Кольцо классов вычетов по модулю m является полем тогда и только тогда, когда m – простое число.

Доказательство: Если m – не простое число, то m=rs для некоторых целых чисел r и s, которые не кратны m. Поэтому 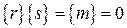, и если класс вычетов {r} обладает обратным 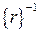, то 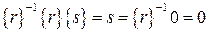, что противоречит предположению. Поэтому класс вычетов {r} не может иметь обратного и кольцо классов вычетов не является полем.

Теперь остается показать, что если m – простое число, то для каждого класса вычетов, кроме 0(идеала), существует обратный. Каждый такой класс вычетов содержит целое число s, которое меньше чем m и не равно 0. Поскольку 1 совпадает с обратным к ней элементом, можно предположить, что s>1. Так как m по предположению – простое число, то наибольший общий делитель s и m должен быть равен либо m, либо 1. Но m>s, и, следовательно, s не может делиться на m. Поэтому НОД m и s равен 1. В силу соотношения (i.2): 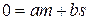. И отсюда следует, что 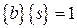, т.е. класс вычетов {b} является обратным к классу вычетов {s}.

Построенные таким образом поля называются кратными полями или полями Галуа из p элементов GF(p).