Понятие идеала. Классы вычетов. Кольцо классов вычетов.

Идеалом I называется подмножество элементов кольца R, обладающее следующими двумя свойствами:

1. I является подгруппой аддитивной группы кольца R.

2. Для любого элемента a из I и любого элемента r из R произведения ar и ra принадлежат I.

Пример:

В кольце из положительных и отрицательных чисел и нуля множество всех чисел, кратных некоторому целому числу, образует идеал.

Поскольку идеал является подгруппой, то по нему могут быть образованы смежные классы. В этом случае смежные классы называются классами вычетов. Идеал образует первую строку разложения с нулевым элементом слева. Далее, любой элемент кольца, не принадлежащий идеалу, может быть выбран в качестве образующего первого класса вычетов, а остальные элементы класса строятся прибавлением образующего к каждому элементу идеала:

, , , …

, , , …

, , , …

.

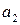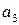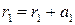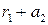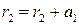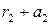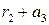Первыми элементами в каждой строке являются, как и прежде, элементы, не использованные в предыдущих строках. Все свойства смежных классов верны также для классов вычетов. В частности, поскольку групповая операция сложения коммутативна, идеал является нормальным делителем, и сложение классов может быть определено как

,

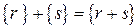где {r} обозначает класс вычетов, содержащий r. При таком определении классы вычетов образуют аддитивную группу (факторгруппу).

Можно также определить умножение классов вычетов следующим образом:

.

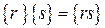Это определение справедливо только в том случае, если независимо от выбора представителей в классах вычетов, которые должны быть перемножены, данное соотношение определяет в качестве произведения один и тот же класс вычетов. Или, другими словами, если r и r’ принадлежат одному и тому же классу вычетов, то произведения rs и r’s должны принадлежать одному и тому же классу вычетов. Это условие будет выполняться тогда и только тогда, когда элемент r’s’-rs принадлежит идеалу. Можно записать

r’s’ – rs = r’s’ - r’s + r’s – rs = r’(s’ - s) + (r’ - r)s.

Поскольку элементы s’-s и r’-r принадлежат идеалу, то каждое из двух слагаемых в правой части этого равенства тоже принадлежит идеалу, и, следовательно, идеалу принадлежит элемент r’s’-rs. Таким образом, определение умножения классов вычетов имеет смысл. Для классов вычетов справедливы ассоциативный и дистрибутивный законы:

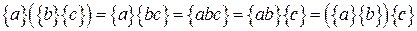
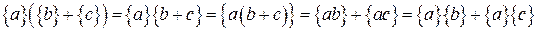
Для них также справедлив дистрибутивный закон для умножения справа. Из всего этого следует теорема:

Теорема 1: Классы вычетов по идеалу в некотором кольце образуют кольцо.

Данное кольцо называется кольцом вычетов.

Пример:

В кольце всех целых чисел рассмотрим идеал, образуемый всеми четными целыми числами. Тогда будет два класса вычетов {0}, {1}. В этом случае с арифметической точки зрения кольцо классов вычетов определяет арифметику по модулю два.