Идеалы многочленов и классы вычетов.

Рассмотрим многочлены f(X) от одного неизвестного (переменного) X с коэффициентами из некоторого поля F:

.

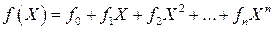Степенью многочлена называется наибольшая степень X в слагаемом с ненулевым коэффициентом. Степень нулевого многочлена равно 0. Многочлен называется нормированным, если коэффициент при наивысшей степени X равен 1. Многочлены можно складывать и умножать обычным путем. Они образуют кольцо.

Если r(x), s(x) и t(x) – многочлены и r(x)s(x) = t(x), то говорят, что многочлен t(x) делится на многочлен r(x) или что многочлен r(x) является делителем многочлена t(x).

Неприводимый многочлен – многочлен p(x) степени n, который не делится ни на какой многочлен степени, меньшей, чем n, но большей чем 0.

НОД двух многочленов – нормированный многочлен наибольшей степени, который является делителем для обоих многочленов.

Два многочлена являются взаимно простыми, если их НОД равен 1.

Степень произведения двух многочленов равна сумме их степеней. Ненулевой многочлен степени 0 является элементом поля и поэтому имеет обратный элемент, но многочлены более высоких степеней не имеют обратных.

Если s(x) делится на r(x) и r(x) делится на s(x), то они отличаются самое большее множителем, который является элементом поля.

Пример:

ax², bx², а и в – элементы поля.

Для любой пары многочленов s(x) и d(x) существует единственная пара многочленов q(x) и r(x), таких, что

,

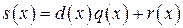где q(x) – частное, r(x) – остаток и степень r(x) меньше степени d(x).

Пример:

GF(2)

x3(+)x2(+)1 / x(+)1

x3(+)x2 / x2

---------------------------------

x3(+)x2(+)1= (x(+)1) x2(+) 1

s(x) d(x) q(x) r(x)

В предположении, что делитель имеет первую степень, т.е. d(x) = x - a, можно получить несколько важных результатов о свойствах кольца многочленов.

Пусть

.

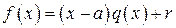Поскольку многочлен r должен иметь степень, меньшую, чем степень делителя, он должен иметь степень равную 0, т.е. должен быть элементом поля. Подставляя в это равенство a вместо x получим

.

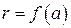Если f(a) = 0, т.е. если a – корень многочлена f(x), то r=0 и многочлен (x-a) является многочленом f(x). Таким образом, каждому корню многочлена f(x) однозначно соответствует множитель первой степени. Поскольку степень произведения многочленов равно сумме степеней множителей, степень f(x) по крайней мере не меньше числа корней многочлена f(x).

НОД d(x) двух многочленов r(x) и s(x) всегда может быть представлен в виде

,

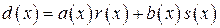где a(x) и b(x) – многочлены.

Теорема 4: Совокупность многочленов образует идеал тогда и только тогда, когда она содержит все многочлены, кратные некоторому многочлену.

Идеал, состоящий из всех многочленов, кратных f(x) обозначается через (f(x)). Кольцо классов вычетов, образованных по этому идеалу, называется кольцом многочленов по модулю f(x).

Теорема 5: Каждый класс вычетов по модулю многочлена f(x) степени n содержит либо 0, либо многочлен степени, меньшей, чем n. Нуль является элементом идеала, а многочлены степеней, меньших, чем n, принадлежат различным классам вычетов.

Пример:

Идеал из чисел, кратных 3:

0 3 -3 6 -6 9 -9 … ® {0}

1 4 -2 7 -5 10 -8 … ® {1}

2 5 -1 8 -4 11 -7 … ® {2}

Классы вычетов по модулю x²+1 и GF(2):

0 x²+1 x(x²+1) (x+1)(x²+1) … ® {0}

1 x² x³+x+1 x³+x²+x … ® {1}

x x²+x+1 x³ x³+x²+1 … ® {x}

x+1 x²+x x³+1 x³+x² … ® {x+1}

Неприводимый многочлен – многочлен p(x) степени n, который не делится ни на какой многочлен степени, меньшей, чем n, но большей чем 0.

НОД двух многочленов – нормированный многочлен наибольшей степени, который является делителем для обоих многочленов.

Два многочлена являются взаимно простыми, если их НОД равен 1.

Степень произведения двух многочленов равна сумме их степеней. Ненулевой многочлен степени 0 является элементом поля и поэтому имеет обратный элемент, но многочлены более высоких степеней не имеют обратных.

Если s(x) делится на r(x) и r(x) делится на s(x), то они отличаются самое большее множителем, который является элементом поля.

Пример:

ax², bx², а и в – элементы поля.

Для любой пары многочленов s(x) и d(x) существует единственная пара многочленов q(x) и r(x), таких, что

,

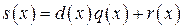где q(x) – частное, r(x) – остаток и степень r(x) меньше степени d(x).

Пример:

GF(2)

x3(+)x2(+)1 / x(+)1

x3(+)x2 / x2

---------------------------------

x3(+)x2(+)1= (x(+)1) x2(+) 1

s(x) d(x) q(x) r(x)

В предположении, что делитель имеет первую степень, т.е. d(x) = x - a, можно получить несколько важных результатов о свойствах кольца многочленов.

Пусть

.

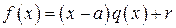Поскольку многочлен r должен иметь степень, меньшую, чем степень делителя, он должен иметь степень равную 0, т.е. должен быть элементом поля. Подставляя в это равенство a вместо x получим

.

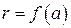Если f(a) = 0, т.е. если a – корень многочлена f(x), то r=0 и многочлен (x-a) является многочленом f(x). Таким образом, каждому корню многочлена f(x) однозначно соответствует множитель первой степени. Поскольку степень произведения многочленов равно сумме степеней множителей, степень f(x) по крайней мере не меньше числа корней многочлена f(x).

НОД d(x) двух многочленов r(x) и s(x) всегда может быть представлен в виде

,

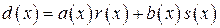где a(x) и b(x) – многочлены.

Теорема 4: Совокупность многочленов образует идеал тогда и только тогда, когда она содержит все многочлены, кратные некоторому многочлену.

Идеал, состоящий из всех многочленов, кратных f(x) обозначается через (f(x)). Кольцо классов вычетов, образованных по этому идеалу, называется кольцом многочленов по модулю f(x).

Теорема 5: Каждый класс вычетов по модулю многочлена f(x) степени n содержит либо 0, либо многочлен степени, меньшей, чем n. Нуль является элементом идеала, а многочлены степеней, меньших, чем n, принадлежат различным классам вычетов.

Пример:

Идеал из чисел, кратных 3:

0 3 -3 6 -6 9 -9 … ® {0}

1 4 -2 7 -5 10 -8 … ® {1}

2 5 -1 8 -4 11 -7 … ® {2}

Классы вычетов по модулю x²+1 и GF(2):

0 x²+1 x(x²+1) (x+1)(x²+1) … ® {0}

1 x² x³+x+1 x³+x²+x … ® {1}

x x²+x+1 x³ x³+x²+1 … ® {x}

x+1 x²+x x³+1 x³+x² … ® {x+1}