Синдромное декодирование.
Предположим, что линейный код является нулевым пространством матрицы H размерности ( 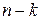 )*n. Для любого любого полученного на выходе вектора v вектор
)*n. Для любого любого полученного на выходе вектора v вектор  с
с 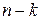 компонентами называется синдромом. Поскольку рассматриваемый код – это нулевое пространство матрицы H, то некоторый вектор является словом тогда и только тогда, когда его синдром равен нулю.
компонентами называется синдромом. Поскольку рассматриваемый код – это нулевое пространство матрицы H, то некоторый вектор является словом тогда и только тогда, когда его синдром равен нулю.
Теорема 4. Два вектора v1 и v2 принадлежат одному и тому же смежному классу тогда и только тогда, когда их синдромы равны.
Доказательство: Два элемента группы v1 и v2 принадлежат одному и тому же смежному классу тогда и только тогда, когда 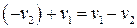 есть элемент подгруппы, которой в данном случае является кодовое векторное пространство. Если кодовое пространство – это нулевое пространство матрицы H, то вектор
есть элемент подгруппы, которой в данном случае является кодовое векторное пространство. Если кодовое пространство – это нулевое пространство матрицы H, то вектор 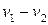 принадлежит кодовому пространству тогда и только тогда, когда
принадлежит кодовому пространству тогда и только тогда, когда
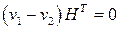 .
.
Поскольку для умножения матриц справедлив дистрибутивный закон, то
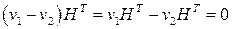 .
.
Таким образом, вектор 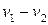 является кодовым вектором тогда и только тогда, когда синдромы векторов v1 и v2 равны.
является кодовым вектором тогда и только тогда, когда синдромы векторов v1 и v2 равны.
Процесс декодирования может быть значительно упрощен за счет использования модифицированной таблицы декодирования. Таблица строится так, что в ней приводятся образующие смежных классов и синдромы для каждого из 2n-k смежных классов. После того как получен вектор, вычисляется его синдром. Затем то таблице отыскивается образующий смежного класса, являющийся предполагаемым набором ошибок и вычитается из полученного вектора. В результате образуется предположительно исходный кодовый вектор.
Пример:
(0000) 1011 0101 1110 (00)
(1000) 0011 1101 0110 (11)
(0100) 1111 0001 1010 (01)
(0010) 1001 0111 1100 (10)
0101®1101®1101 (+) 1000 = 0101
Синдромное декодирование позволяет сократить объем памяти при декодировании. Так, для кода (100,80) необходимо в случае декодировании по лидеру смежного класса 2100 входов, а в случае синдромного декодирования 220 входов.
Коды Хэмминга.
Двоичный код Хэмминга удобнее всего задавать при помощи его проверочной матрицы. Проверочной матрицей кода Хэмминга является матрица, столбцами которой являются все ненулевые наборы разрядности m.
Пример:

Поскольку сумма любых двух столбцов этой матрицы не равна нулю и поскольку единственным отличным от нуля скаляром поля GF(2) является «1», то не существует ни одной нулевой линейной комбинации из двух столбцов матрицы H. Следовательно, нулевое пространство этой матрицы имеет минимальный вес равный 3, и является кодом, исправляющим все одиночные ошибки. Другие важные параметры кода Хэмминга:
- длина кодового вектора : 2m-1;
- число проверочных символов : m;
- число информационных символов : 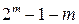 /
/
Поскольку все 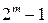 векторов, задающих одиночные ошибки принадлежат различным смежным классам, то этими смежными классами и кодовым пространством исчерпываются все 2m смежных классов.
векторов, задающих одиночные ошибки принадлежат различным смежным классам, то этими смежными классами и кодовым пространством исчерпываются все 2m смежных классов.
Таким образом, код Хэмминга является совершенным. Линейный код, совокупность образующих смежных классов которого в точности совпадает с совокупностью всех последовательностей веса t или меньше, называется совершенным.
Можно построить код Хэмминга любой длины n, Если выбрать матрицу H для наименьшего значения m, удовлетворяющего условию  , а затем отбросить все лишние столбцы, оставив n столбцов. При этом можно выбрать столбцы таким образом, чтобы получился квазисовершенный код.
, а затем отбросить все лишние столбцы, оставив n столбцов. При этом можно выбрать столбцы таким образом, чтобы получился квазисовершенный код.
Добавлением к двоичному коду Хэмминга одного проверочного соотношения, проверяющего на четность совокупность всех символов кода можно получить код с минимальным весом, равным 4, т.е. так называемый расширенный код Хэмминга.
Пример:
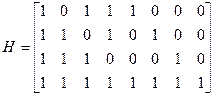 .
.
Декодирование такого кода осуществляется следующим образом:
- Если синдром равен 0, то предполагается, что ошибок не было.
- Если проверка по всем символам, соответствующая последней строке матрицы H дает «1» (проверка на четность), то предполагается, что произошла одна ошибка и слово можно исправить.
Если проверка на четность дает «0», а хотя бы один из остальных проверочных символов равен «1», то обнаружена неисправимая ошибка.
Коды Рида-Маллера.
Достоинства: можно получить большое Хэммингово расстояние и легко поддаются декодированию.
Для любых m и r<m существует код Рида-Маллера, для которого:
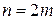 – разрядность кодового вектора,
– разрядность кодового вектора,
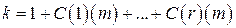 – число информационных бит,
– число информационных бит,
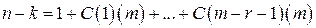 – число проверочных бит,
– число проверочных бит,
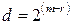 – минимальный вес кодового слова.
– минимальный вес кодового слова.
Рассмотрим следующую совокупность векторов над полем из двух элементов (0 и 1).
Пусть V0 – вектор длины 2m, все компоненты которого равны 1, V1,V2,…, Vm – строки матрицы, столбцами которой являются все возможные двоичные наборы длины m. Определим следующим образом векторное произведение двух векторов:
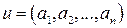 ,
, 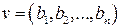
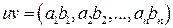 .
.
Рассмотрим совокупность векторов, образованную произведениями векторов vi, взятых по два, три, четыре и т.д. вплоть до m.
v0 = ( 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 )
v4 = ( 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 )
v3 = ( 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 )
v2 = ( 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 )
v1 = ( 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 )
v4v3 = ( 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 )
v4v2 = ( 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 1 )
v4v1 = ( 0 0 0 0 0 0 0 0 0 1 0 1 0 1 0 1 )
v3v2 = ( 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 )
v3v1 = ( 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 1 )
v2v1 = ( 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 )
v4v3v2= …
v4v3v1= …
v4v2v1= …
v3v2v1= …
v4v3v2v1= …
Код Рида-Маллера порядка r определяется как код, базисом которого являются вектор v0,v1,…,vm и все векторные произведения из r или меньшего числа этих векторов. Очевидно, что скалярное произведение двух векторов равно 0, если число единиц в векторном произведении четно и равно 1, если оно нечетно.
Для любого вектора v v2=v. Единственным произведением, содержащим нечетное число единиц, является произведение всех векторов v1,…,vm. Векторное произведение любого вектора из базиса кода порядка r на любой вектор из базиса кода порядка m-r-1 является вектором из базиса кода порядка m-1 и в нем содержится четное число единиц. Таким образом, любой вектор, принадлежащий коду порядка r, ортогонален любому базисному вектору, являющемуся произведением m-r-1 или меньшего числа векторов v1,…,vm. Из этого также следует, что код Рида-Маллера порядка r является нулевым пространством матрицы, образованной векторами v0,v1,…,vm и всеми векторными произведениями этих векторов в количестве не более чем m-r-1, взятыми в качестве ее строк.
Важнейшая особенность кодов Рида-Маллера состоит в том, что декодирование для них может быть проведено достаточно простым способом.
Пример:
m=4, r=2, (16,11)
Информационные символы этого кода кодируются следующим вектором:

Задача состоит в том, чтобы определить значения a по полученному вектору, несмотря на возможные ошибки. Очевидно, что сумма первых четырех компонент как элементов поля из двух элементов (0 и 1) равна нулю для всех базисных векторов, за исключением v2v1. Таким образом, если ошибок не было, то:
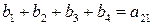
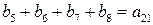
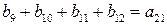
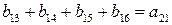
В общем случае можно записать 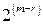 независимых соотношений. Ошибки могут сделать некоторые из этих соотношений несправедливыми, но каждая ошибка влияет только на одно из соотношений. Следовательно, если выбрать a21 равным величине, появляющейся наиболее часто в выражениях, то при любой комбинации из
независимых соотношений. Ошибки могут сделать некоторые из этих соотношений несправедливыми, но каждая ошибка влияет только на одно из соотношений. Следовательно, если выбрать a21 равным величине, появляющейся наиболее часто в выражениях, то при любой комбинации из 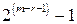 или меньшего числа ошибок значение a21 будет декодировано правильно. Аналогичным образом определяются a31, a32, a41, a43. После того как они определены, выражение
или меньшего числа ошибок значение a21 будет декодировано правильно. Аналогичным образом определяются a31, a32, a41, a43. После того как они определены, выражение

может быть вычтено из полученного вектора. Тогда, если ошибок не было, останется вектор
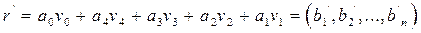 ,
,
так, что следующая совокупность коэффициентов может быть определена аналогичным путём:
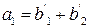
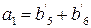
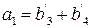
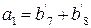
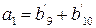
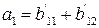

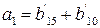
Идентичные уравнения можно записать для a2, a3, a4. Если предположить, что ошибок не было, то
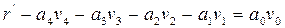 .
.
Этот вектор должен быть нулевым, если a0=0 и единичным, если a0=1, поэтому a0 нужно выбирать равным тому из этих элементов, который появляется в векторе чаще.
Поскольку при такой системе декодирования могут быть исправлены все комбинации из 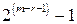 или меньшего числа ошибок, то минимальное расстояние должно быть равно самое меньшее
или меньшего числа ошибок, то минимальное расстояние должно быть равно самое меньшее 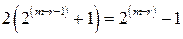 , а так как все кодовые векторы имеют четный вес, то оно должно быть равно самое меньшее
, а так как все кодовые векторы имеют четный вес, то оно должно быть равно самое меньшее 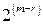 .
.
Схему для определения того, суммы каких именно символов полученного вектора должны быть равны заданному информационному символу, можно описать следующим образом. Расположим символы в каждом из первоначальных векторов v1,…,vm, и назовем компоненту, соответствующую j-ому нулю в векторе vi, и компоненту, соответствующую j-ой единице в векторе vi, парными компонентами вектора vi. Тогда 2(m-1) сумм парных компонент vi используются для определения ai. Далее, каждая из 2(m-2) сумм четырех компонент, используемых для определения aij, образуется некоторыми двумя парными компонентами вектора vi и парными для этих уже выбранных компонент компонентами вектора vj. Аналогично каждое соотношение, определяющее aijk, представляет собой сумму некоторых парных компонент вектора vi плюс сумму компонент вектора vj, парных к этим компонентам, и сумму компонент вектора vk, парных к уже выбранным компонентам, так, что в каждой сумме получается всего 8 слагаемых. Этот процесс можно продолжить аналогичным образом.
Пример:
a3:
v3=(0000111100001111)
a3=(b1+b5)=(b2+b6)=(b3+b7)=(b4+b8)=(b9+b13)=(b10+b14)=(b11+b15)=(b12+b16).
v3=(0000111100001111)
v1=(0101010101010101)
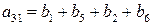
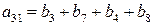
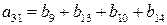
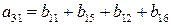
Дата добавления: 2016-06-13; просмотров: 1560;
