Описание линейных кодов при помощи матриц.

Любое множество базисных векторов линейного кода V можно рассматривать как строки матрицы G, называемой порождающей матрицей кода V. Пространство строк матрицы G является линейным кодом V, и вектор является кодовым вектором тогда и только тогда, когда он является линейной комбинацией строк матрицы G. Если размерность векторного пространства V равна k, то число строк матрицы G равно k. (Число строк равно рангу матрицы G, потому что строки матрицы должны быть линейно независимыми). Различные линейные комбинации строк дают различные кодовые векторы, и так как имеется k коэффициентов с q возможными значениями для каждого, то пространство V содержит всего q^k кодовых векторов. Такой код называется (n,k)-кодом.

Пример:

Код V₁ (пред. пример) является пространством строк матрицы:

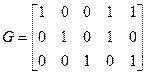
Если V есть подпространство размерности k, то его нулевое пространство является векторным пространством V’ размерности n-k. Таким образом, может быть построена матрица H ранга 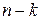, строками которой является базис пространства V’. Для любого v из V будет справедливо следующее соотношение:

,

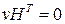которое означает, что для каждой строки матрицы H в случае двоичного кода, число единиц вектора v, которым соответствуют единицы в строке матрицы H, должно быть четным. Матрица H называется проверочной матрицей кода V. Для порождающей и проверочной матриц кода справедливо также соотношение:

,

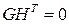где 0 обозначает нулевую матрицу размерности k x .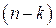

Пример:

Нулевое пространство V₂ для векторного пространства V₁ (пред. пример) содержит четыре вектора:

(00000)

(11010)

(10101)

(01111)

Эти четыре вектора образуют векторное пространство. Первые два ненулевых вектора линейно независимы и образуют базис. Таким образом, V₁ является пространством строк матрицы

.

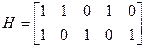Код V₁ представляет собой нулевое пространство этой матрицы.

В общем случае двоичный линейный код при помощи матриц описывается так: в конечном пространстве n-мерных векторов над полем Галуа GF(2) выбираем множество векторов, которые образуют множество кодовых слов. Это множество есть подпространство V (код V). Базисом подпространства V является множество линейно независимых векторов из V, которые порождают само подпространство. Матрица G, строками которой являются базисные вектора, есть порождающая матрица кода V. Количество k строк матрицы G равно размерности подпространства V. Сам код носит название 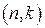-кода. Для подпространства V существует нулевое пространство V’ размерностью 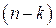. Базис пространства V’ образует строки проверочной матрицы H для кода V. При этом должно выполняться условие, что .

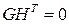Пример: Конечное пространство из 3-ех мерных векторов над полем GF(2) представляет собой следующее множество: (000), (001), (010), (011), (100), (101), (110), (111). Выделим их это векторного пространства подпространство V, элементами которого будут являться кодовые слова кода проверки на четность: (000), (011), (101), (110). Два первых ненулевых линейно независимых вектора образуют базис этого подпространства: (011), (101) и являются соответственно строками порождающей матрицы G кода проверки на четность. Из всего векторного пространства выделим множество векторов, которые образуют нулевое пространство V’ для подпространства V: (000), (111). Базисом этого пространства является один вектор (111), который и образует единственную строку проверочной матрицы H для кода V. При этом:

, , .

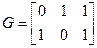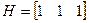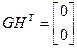Если векторное пространство V является линейным кодом, то его нулевое пространство V’ тоже является линейным кодом. Они называются двойственными (дуальными) кодами. Если V это 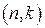-код, то V’ – 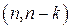-код.

Теорема 1. Пусть V – линейный код, который совпадает с нулевым пространством матрицы H. Тогда каждому кодовому слову веса Хэмминга w соответствует соотношение линейной зависимости, связывающее w столбцов матрицы H, и, наоборот, каждому соотношению линейной зависимости, включающему w столбцов матрицы H, соответствует кодовое слово веса w.

Доказательство: Вектор 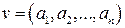является кодовым словом тогда и только тогда, когда vH^T=0, или, если обозначить i-ый вектор столбец матрицы через h_i, тогда и только тогда, когда

.

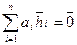Это соотношение линейной зависимости связывает столбцы матрицы H, причем число столбцов матрицы H, которые входят с ненулевыми коэффициентами, равно числу ненулевых компонент a_i вектора .v Это число в точности равно весу вектора v. Аналогично коэффициенты любого соотношения линейной зависимости, связывающего столбцы матрицы H, являются компонентами вектора, который должен принадлежать нулевому пространству матрицы H.

Следствие: Блоковый код, являющийся нулевым пространством матрицы H, имеет минимальный вес, равный самое малое w, тогда и только тогда, когда любая совокупность w-1 или меньшего числа столбцов H является линейно независимой.