Метрики Хэмминга и Ли.

Вес Хэмминга вектора v, обозначаемый как w(v), определяется как число ненулевых компонент этого вектора.

Расстояние Хэмминга между двумя векторами v1 и v2 равно числу компонент, которыми они отличаются: 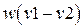. Если v1 и v2 являются кодовыми словами линейного кода, то разность 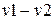также должна быть кодовым словом, т.к. множество всех кодовых слов есть векторное пространство. Следовательно, расстояние между двумя кодовыми векторами равно весу некоторого третьего кодового вектора, и минимальное расстояние для линейного кода равно минимальному весу его ненулевых векторов.

Пример: q=2, n=5.

Совокупность векторов:

(00000)

(10011)

(01010)

(11001)

(00101)

(10110)

(01111)

(11100)

образует векторное пространство V₁ (линейный двоичный код). Минимальный вес равен 2, следовательно, минимальное расстояние равно 2.

Вес Ли набора 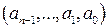длины n, где элементы a_i выбираются из множества 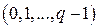, а q – произвольное положительное число, определяется как:

,

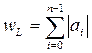где

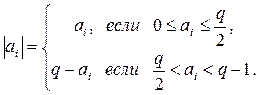
Расстоянием Ли между двумя наборами длины n называется вес Ли разности этих наборов. При q=2 и q=3 расстояние Ли и расстояние Хэмминга совпадают; при q>3 расстояние Ли между двумя наборами длины n больше или равно расстоянию Хэмминга между этими наборами.

Пример: q=5, n=6.

Расстояние Ли между двумя наборами длины 6 A=(200234), B=(204000) равно весу набора, составленного из разностей соответствующих компонент по модулю 5:

A-B=(001234).

Тогда w_L(A-B)=0+0+1+2+2+1=6.