Простые коды с проверкой на четность.

Теория кодирования. Основные понятия.

Рассматриваемый канал передачи данных – дискретный.

Данные передаются в виде двоичной информации (последовательность 0 и 1). Информация передается по каналу, подверженному случайным ошибкам.

Задача кодирования – добавление к информационным символам дополнительных символов, чтобы принимающая сторона могла обнаружить и исправить ошибки.

2.1. Понятие -кодов

Классификация кодов:

- блоковые коды;

- древовидные коды.

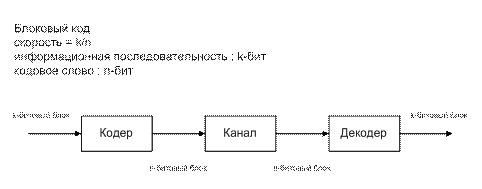
Блоковые коды определяются над произвольным конечным алфавитом, состоящего из 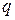символов .

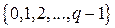Определение: Блоковый код мощности 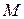над алфавитом из 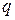символов определяется как множество из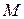 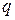-ичных последовательностей длины 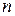, называемых кодовыми словами.

Если 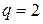, то символы называются битами. Обычно .

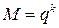Скорость 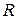блокового кода определяется равенством: .

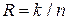Древовидные коды оперируют с бесконечными последовательностями информационных символов, поступающих со скоростью 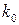символов за один интервал времени. Это отображается в непрерывную последовательность символов кодового слова со скоростью 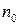символов за один интервал времени (кадр). При этом скорость кода вычисляется как .

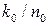Основные характеристики блоковых кодов:

- длина блока ;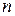

- длина информационной части ;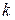

- минимальное расстояние .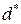

Понятие расстояния

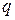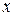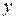Определение: Расстоянием по Хэммингу между двумя -ичными последовательностями и длины 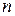называется число позиций, в которых они различны. Это расстояние обозначается как .

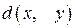Пример: Пусть 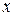=011101, 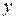=110100, тогда 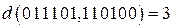. Пусть 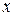=52204, 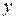=32203, тогда .

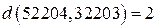Определение: Пусть 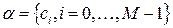– код. Тогда минимальное расстояние 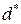кода a равно наименьшему из всех расстояний по Хэммингу между различными парами кодовых слов:

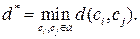
-код с минимальным расстоянием 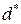называется также 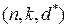-кодом.

Пример:

Код (3,3) может быть описан как код (3,3,1), т.к. минимальное расстояние по Хэммингу в счетчиковой последовательности от 000 до 111 равно 1:

Тема 3: Простейшие коды.

Простые коды с проверкой на четность.

Высокоскоростные коды с плохими корректирующими характеристиками. К заданным 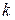информационным битам дописывается 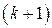-й бит так, чтобы полное число единиц в кодовом слове было четным (нечетным) (это есть бит проверки на четность (нечетность)).

Пример:

000 – 000(0);

001 – 001(1);

010 – 010(1);

011 – 011(0); и т.д.

Это 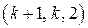-код или 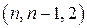-код.

Минимальное расстояние кода равно 2. Никакие ошибки исправлены быть не могут. Используется только для обнаружения ошибок нечетной кратности.