Простые коды с повторением
Низкоскоростные коды с хорошими корректирующими характеристиками. Один информационный символ повторяется n раз.
Пример:
0 – 000;
1 – 111.
Это 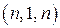 -код. Минимальное расстояние
-код. Минимальное расстояние 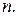 Может быть исправлено
Может быть исправлено 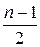 ошибок.
ошибок.
Коды Хэмминга
Данные коды позволяют исправлять одну ошибку. Описание кода: для каждого 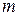 существует
существует 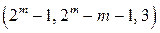 -код Хэмминга. При больших
-код Хэмминга. При больших 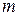 скорость кода близка к 1.
скорость кода близка к 1.
Пусть дан код Хэмминга (7,4,3) для  . Его можно описать при помощи следующей реализации. При заданных четырех информационных битах
. Его можно описать при помощи следующей реализации. При заданных четырех информационных битах 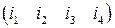 вычисляются три проверочных бита согласно следующим равенствам:
вычисляются три проверочных бита согласно следующим равенствам:
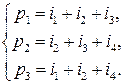
Операция + означает сложение по модулю 2, т.е. 0+0=0, 0+1=1, 1+0=1, 1+1=1. Кодовое слово v для передачи по дискретному каналу представляет собой блок из 7 битов:
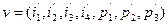 .
.
По мере поступления кодового слова получателю декодер канала на основе информационных и проверочных битов вычисляет значения битов синдрома 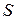 :
:
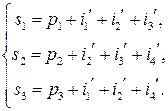
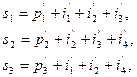
Такой синдром нацелен на обнаружения факта наличия только однократной ошибки. Возможные значения битов синдрома являются уникальными для всевозможных конфигураций однократной ошибки в пределах переданного кодового слова. В случае отсутствия ошибки в слове, декодер канала всегда вычисляет синдром равный нулю. Данное свойство кодов Хэмминга позволяет конструировать цифровую логику, которая по ненулевому значению синдрома способна произвести коррекцию ошибочного бита. Для этого необходимо, чтоб ненулевое значение синдрома 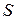 представляло собой адрес ошибочного бита в переданном пакете. Так, всевозможные значения синдрома
представляло собой адрес ошибочного бита в переданном пакете. Так, всевозможные значения синдрома 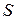 выглядят следующим образом:
выглядят следующим образом:
| p1 | p2 | i3 | p3 | i1 | i4 | i2 | |
| s1 = | |||||||
| s2 = | |||||||
| s3 = |
Размещение информационных и проверочных битов по адресам равным значениям синдрома 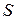 в случае однократной ошибки позволяет автоматически производить их коррекцию. Помимо коррекции однократных ошибок коды Хэмминга позволяют обнаруживать двукратные ошибки. Существует еще класс расширенных кодов Хэмминга. Они представляют собой
в случае однократной ошибки позволяет автоматически производить их коррекцию. Помимо коррекции однократных ошибок коды Хэмминга позволяют обнаруживать двукратные ошибки. Существует еще класс расширенных кодов Хэмминга. Они представляют собой 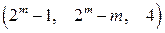 -коды. В отличие от обычных кодов добавляется еще один дополнительный разряд проверки на четность. Такие коды позволяют корректировать однократные ошибки и обнаруживать двукратные и ошибки нечетных кратностей.
-коды. В отличие от обычных кодов добавляется еще один дополнительный разряд проверки на четность. Такие коды позволяют корректировать однократные ошибки и обнаруживать двукратные и ошибки нечетных кратностей.
Дата добавления: 2016-06-13; просмотров: 1820;
