Декодирование линейных кодов.

Пусть V – линейный 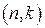-код, h – нулевой вектор и h₂, h_{3, …,} h_q^k– остальные кодовые векторы. Тогда таблица декодирования можно составить следующим образом. Кодовые векторы располагаются в виде строки с нулевым вектором слева. Затем один из наборов, не содержащийся в этой строке и имеющий разрядность n, например g_i помещается под вектором h. Далее строка заполняется так, чтобы под каждым кодовым вектором h_i помещался вектор 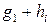. Аналогично в первый столбец очередной строки помещается вектор g₂ и строка заполняется таким же способом. Процесс продолжается до тех пор, пока каждый возможный набор длины n не появится где-нибудь в таблице. Данная таблица называется стандартным расположением и совпадает с таблицей смежных классов.

Теорема 3. Если стандартное расположение используется как таблица декодирования для блокового кода, то по полученному вектору u будет правильно декодирован переданный вектор v тогда и только тогда, когда набор ошибок 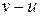является образующим смежного класса.

Доказательство: Если 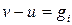, где g_i – образующий i-го смежного класса, то вектор 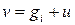должен находиться в стандартом расположении в i-м смежном классе под кодовым словом u и поэтому будет правильно декодирован. Если же вектор 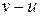не является образующим смежного класса, то вектор v должен находиться в некотором классе j с образующим g_j. Тогда вектор v расположен в j-й строке, но не под вектором u, потому что .

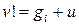Пример:

*0000 *1011 *0101 *1110

1000 0011 1101 0110

0100 1111 0001 1010

0010 1001 0111 1100

а) 1011 ® 1001 ® 1001 (+) 0010 = 1011.

б) 0101 ® 0100 ® 0100 (+) 0100 = 0000 – неверно.

Другим важным случаем декодирования линейных кодов является синдромное декодирование.