Графические методы анализа переходных процессов в нелинейных цепях

Графическими называются методы, в основе которых лежат графические построения на плоскости. По сравнению с рассмотренными выше аналитическими методами они обладают следующими основными преимуществами:
- отсутствием принципиальной необходимости в аналитическом выражении характеристики нелинейного элемента, что устраняет погрешность, связанную с ее аппроксимацией;
- возможностью проведения расчетов при достаточно сложных формах кривых нелинейных характеристик.
Главный недостаток графических методов заключается в получении решения для конкретных значений параметров цепи.
Основными графическими методами, используемыми при решении электротехнических задач, являются:
Метод графического интегрирования
Метод графического интегрирования основан на графическом подсчете определенного интеграла и заключается в последовательном нахождении площадей под соответствующей подынтегральной функции кривой. Он применяется для анализа электрических цепей, переходные процессы в которых описываются дифференциальными уравнениями первого порядка с разделяющимися переменными.
Метод изоклин
Данный метод является одним из наиболее широко используемых графических методов приближенного интегрирования. Он непосредственно используется для решения уравнений первого порядка вида 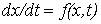 и при этом включает в себя в общем случае следующие этапы:
и при этом включает в себя в общем случае следующие этапы:
в плоскости 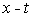 по уравнениям изоклин
по уравнениям изоклин 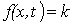 (изоклина - линия равного наклона, вдоль которой функция
(изоклина - линия равного наклона, вдоль которой функция 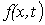 имеет постоянное значение, т.е. геометрическое место точек, для которых
имеет постоянное значение, т.е. геометрическое место точек, для которых 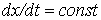 ) строятся изоклины для различных значений углового коэффициента
) строятся изоклины для различных значений углового коэффициента 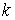 ;
;
вдоль каждой изоклины наносятся черточки с наклоном, определяемым соответствующим значением 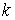 ;
;
от точки 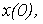 соответствующей начальному условию, строится интегральная кривая так, чтобы она пересекала каждую изоклину параллельно нанесенным на ней черточкам; полученная кривая является графиком искомой зависимости
соответствующей начальному условию, строится интегральная кривая так, чтобы она пересекала каждую изоклину параллельно нанесенным на ней черточкам; полученная кривая является графиком искомой зависимости 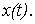
Дата добавления: 2017-02-04; просмотров: 669;
