Эквивалентность линейных кодов.
Если V – пространство строк матрицы G, то код V’ эквивалентен коду V тогда и только тогда, когда V’ – пространство строк матрицы G’, полученной из матрицы G перестановкой столбцов.
Любая порождающая матрица G комбинаторно-эквивалентна (если одна матрица может быть получена из другой путем комбинации элементарных операций над строками и перестановок столбцов, то эти две матрицы называются комбинаторно-эквивалентыми) некоторой матрице G’, имеющей ступенчатую каноническую форму.
Матрица G’ может быть получена из матрицы G следующим образом: начиная с первой строки с каждой из k строк матрицы G произведем следующие операции:
1. В i-ой строке найдется по меньшей мере один ненулевой элемент, поскольку строки линейно независимы. Предположим, что первый отличный от нуля элемент находится в j-ом столбце. Разделим каждый элемент i-ой строки на aij. В результате новый элемент матрицы aij’ станет равен единице.
2. К каждой l-ой строке (l!=i) прибавим i строку, умноженную на (-alj). В результате в j-ом столбце i-ая строка будет содержать единицу, а все остальные строки - нули.
После того, как эти операции будут проделаны над каждой строкой матрицы, получится матрица G’, содержащая k столбцов, каждый из которых содержит единицу и k-1 нулей, причем единица появится обязательно в каждой строке.
Поскольку G’ может быть получена из G с помощью операций над строками, то они порождают один и тот же код. Далее перестановкой столбцов можно сгруппировать слева k столбцов, содержащих единицы в качестве первых ненулевых элементов, в результате чего получается матрица G’’ следующего вида:

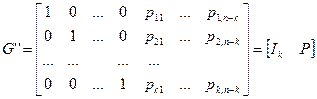
Пусть 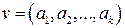 – произвольный набор длины k. Рассмотрим вектор u, являющийся линейной комбинацией строк матрицы G’’ с элементом ai в качестве i-го коэффициента:
– произвольный набор длины k. Рассмотрим вектор u, являющийся линейной комбинацией строк матрицы G’’ с элементом ai в качестве i-го коэффициента: 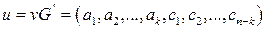 , где
, где
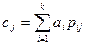 .
.
Таким образом, первые k компонент кодового вектора могут быть произвольно выбранными информационными символами, а каждая из последних 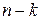 компонент является линейной комбинацией первых k компонент. Благодаря этому кодирование значительно упрощается. Код такого типа называется систематическим; первые k компонент называются информационными символами, а последние
компонент является линейной комбинацией первых k компонент. Благодаря этому кодирование значительно упрощается. Код такого типа называется систематическим; первые k компонент называются информационными символами, а последние 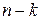 компонент называются избыточными или проверочными символами. Каждый линейный код эквивалентен систематическому коду.
компонент называются избыточными или проверочными символами. Каждый линейный код эквивалентен систематическому коду.
Между матрицами G и H существует связь, которая может быть сформирована следующей теоремой.
Теорема 2. Если V – пространство строк матрицы G=[IkP], где Ik – единичная матрица размерности k x k, а P – матрица размерности k x (n-k), то V является нулевым пространством матрицы H=[-PTIn-k], где In-k – единичная матрица размерности (n-k) x (n-k).
Пример:
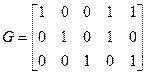 ,
, 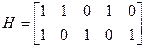
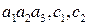 ,
, 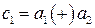 ,
, 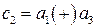 .
.
Дата добавления: 2016-06-13; просмотров: 911;
