Метод вариации произвольных постоянных.
Суть этого метода заключается в том, что решение неоднородного дифференциального уравнения 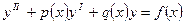 ищется в виде:
ищется в виде: 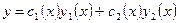 , где
, где 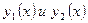 линейно независимые решения однородного уравнения
линейно независимые решения однородного уравнения 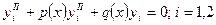 . Остается найти функции
. Остается найти функции 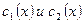 .
.
Подставим выражение 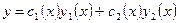 в исходное дифференциальное уравнение, получим:
в исходное дифференциальное уравнение, получим:

Подчеркнутые одной линией слагаемые в сумме дают ноль, поскольку 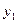 - решение однородного уравнения. По этой же причине, только для функции
- решение однородного уравнения. По этой же причине, только для функции  , в ноль обращается сумма слагаемых, подчеркнутых двойной линией. В результате получаем:
, в ноль обращается сумма слагаемых, подчеркнутых двойной линией. В результате получаем:
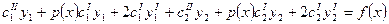 . Перепишем эту строчку в таком виде:
. Перепишем эту строчку в таком виде: 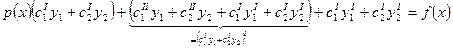 .
.
Потребуем, чтобы 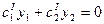 .
.
 . Из этой системы уравнений находим
. Из этой системы уравнений находим 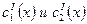 , интегрируя, находим
, интегрируя, находим 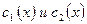 .
.
Получаем общее решение: 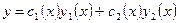 .
.
Пример:найти общее решение уравнения.
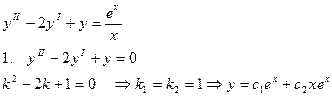
 - два линейно независимых решения.
- два линейно независимых решения.
2. Решение неоднородного уравнения будем искать в виде:
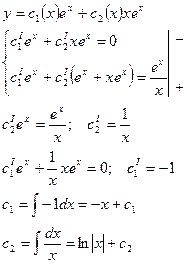
общее решение уравнения: 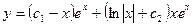 .
.
Метод неопределенных коэффициентов для построения частного решения неоднородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами и специальной правой частью.
Специальной правой частью будем называть функцию  следующего вида:
следующего вида:
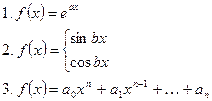
А также их произведения.
В общем виде специальную правую часть можно записать в виде: 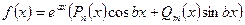 , где
, где 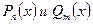 - это многочлены соответственно степеней nи m.
- это многочлены соответственно степеней nи m.
Утверждение:частное решение дифференциального уравнения можно искать в том же виде, который имеет специальная правая часть с неопределенными коэффициентами в многочленах.
Замечание 1:если в специальной правой части фигурируют тригонометрическая функция 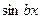 или
или 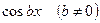 , то в проекте частного решения обязательно следует писать обе тригонометрические функции
, то в проекте частного решения обязательно следует писать обе тригонометрические функции 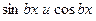 , умноженные на многочлены одной и той же степени (старшей), но с разными неопределенными коэффициентами.
, умноженные на многочлены одной и той же степени (старшей), но с разными неопределенными коэффициентами.
Замечание 2:если число 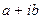 является корнем характеристического уравнения кратности r, то проект частного решения следует целиком домножить на
является корнем характеристического уравнения кратности r, то проект частного решения следует целиком домножить на 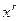 .
.
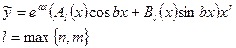 ,
,
r– кратностьь характеристического уравнения.
Неопределенные коэффициенты находятся после подстановки проекта частного решения в исходное дифференциальное уравнение и приравнивания коэффициентов при одинаковых степенях х.
Пример: 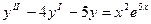 .
.
1. найдем общее решение однородного уравнения:
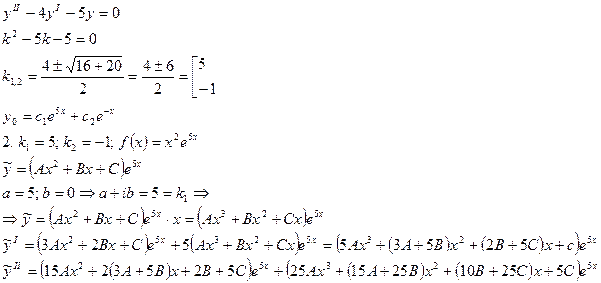 подставляем все это в исходное неоднородное уравнение. Каждое слагаемое будет содержать множитель
подставляем все это в исходное неоднородное уравнение. Каждое слагаемое будет содержать множитель 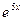 , на который мы сократим.
, на который мы сократим.
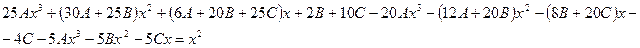 коэффициенты при
коэффициенты при 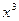 сокращаются, приравняем остальные коэффициенты:
сокращаются, приравняем остальные коэффициенты:
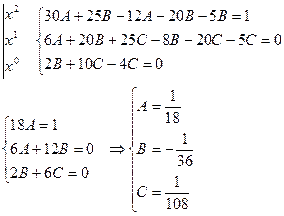
Частное решение: 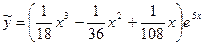 .
.
Общее решение: 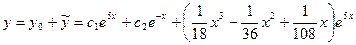 .
.
Дата добавления: 2016-06-24; просмотров: 1433;
