N-мерный вектор и векторное пространство

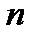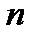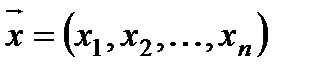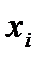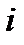Определение. - мерным векторомназывается упорядоченная совокупность действительных чисел, записываемых в виде , где - -я компонента вектора .

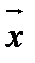Два 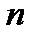- мерных вектора равны тогда и только тогда, когда равны их соответствующие компоненты, т.е.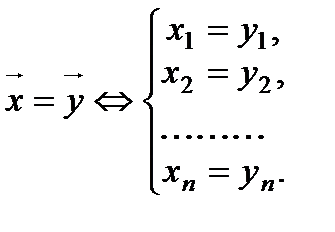

Суммой двух векторов одинаковой размерности 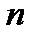называется вектор 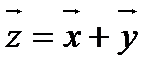, компоненты которого равны сумме соответствующих компонент слагаемых, т.е. .

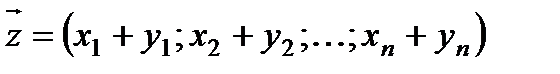Произведением вектора 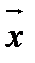на действительно число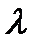 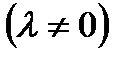называется вектор 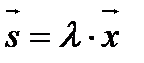, компоненты которого равны произведению 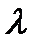на соответствующие компоненты вектора 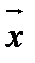, т.е. .

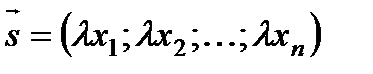Определение. Множество векторов R с действительными компонентами, в котором определены следующие операции:

1) для любых двух элементов 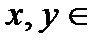R однозначно определён третий элемент 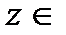R, называемый их суммой, который обозначают 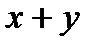(операция сложения векторов)

2)для любого числа 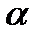и любого элемента 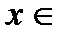R определён элемент 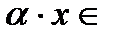R (умножения вектора на число), удовлетворяющее свойствам ниже, рассматриваемым как аксиомы, называется векторным пространством.

Линейные операции над любыми векторами удовлетворяют следующие свойства (аксиомы):

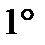
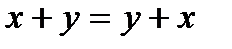- коммутативное (переместительное) свойство суммы;

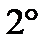
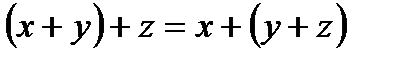- ассоциативное (сочетательное) свойство суммы;

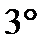
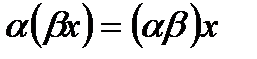- ассоциативное относительно числового множителя;

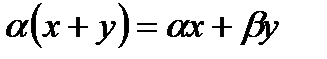- дистрибутивное относительно суммы векторов;

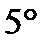
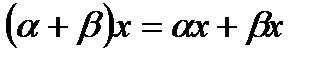- дистрибутивное относительно суммы числовых множителей;

Существует в R нулевой вектор 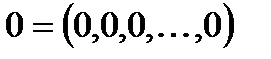такой, что 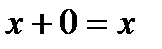для всех 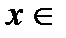R.

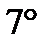Для любого вектора 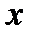существует противоположный вектор 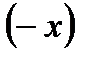такой, что .

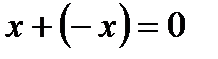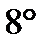
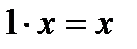для любого вектора .

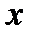Следует отметить, что под 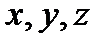можно рассматривать не только векторы, но и элементы любой природы. В этом случае соответствующее множество элементов называется линейным пространством.